
【題目】數學問題:用邊長相等的正三角形、正方形和正六邊形能否進行平面圖形的鑲嵌?
問題探究:為了解決上述數學問題,我們采用分類討論的思想方法去進行探究.
探究一:從正三角形、正方形和正六邊形中任選一種圖形,能否進行平面圖形的鑲嵌?
第一類:選正三角形.因為正三角形的每一個內角是60°,所以在鑲嵌平面時,圍繞某一點有6個正三角形的內角可以拼成一個周角,所以用正三角形可以進行平面圖形的鑲嵌.
第二類:選正方形.因為正方形的每一個內角是90°,所以在鑲嵌平面時,圍繞某一點有4個正方形的內角可以拼成一個周角,所以用正方形也可以進行平面圖形的鑲嵌.
第三類:選正六邊形.(仿照上述方法,寫出探究過程及結論)
探究二:從正三角形、正方形和正六邊形中任選兩種圖形,能否進行平面圖形的鑲嵌?
第四類:選正三角形和正方形
在鑲嵌平面時,設圍繞某一點有x個正三角形和y個正方形的內角可以拼成個周角.根據題意,可得方程
60x+90y=360
整理,得2x+3y=12.
我們可以找到唯一組適合方程的正整數解為![]() .
.
鑲嵌平面時,在一個頂點周圍圍繞著3個正三角形和2個正方形的內角可以拼成一個周角,所以用正三角形和正方形可以進行平面鑲嵌
第五類:選正三角形和正六邊形.(仿照上述方法,寫出探究過程及結論)
第六類:選正方形和正六邊形,(不寫探究過程,只寫出結論)
探究三:用正三角形、正方形和正六邊形三種圖形是否可以鑲嵌平面?
第七類:選正三角形、正方形和正六邊形三種圖形.(不寫探究過程,只寫結論),
【答案】詳見解析
【解析】
根據題意列出二元一次方程或三元一次方程,求出方程的正整數解,即可得出答案.
解:第五類:設x個正三角形,y個正六邊形,
則60x+120y=360,
x+2y=6,
正整數解是![]() 或
或![]() ,
,
即鑲嵌平面時,在一個頂點周圍圍繞著2個正三角形和2個正六邊形(或4個正三角形和1個正六邊形)的內角可以拼成一個周角,所以用正三角形和正六邊形可以進行平面鑲嵌;
第六類:設x個正方形,y個正六邊形,
則90x+120y+=360,
3x+4y=12,
此方程沒有正整數解,
即鑲嵌平面時,不能在一個頂點周圍圍繞著正方形和正六邊形的內角拼成一個周角,所以不能用正方形和正六邊形進行平面鑲嵌;
第七類:設x個正三角形,y個正方形,z個正六邊形,
則60x+90y+120z=360,
2x+3y+4z=12,
正整數解是![]() ,
,
即鑲嵌平面時,在一個頂點周圍圍繞著1個正三角形、2個正方形、1個正六邊的內角可以拼成一個周角,所以用正三角形、正方形、正六邊形可以進行平面鑲嵌.


科目:初中數學 來源: 題型:
【題目】如圖,把一個轉盤分成六等份,依次標上數字1、2、3、4、5、6,小明和小芳分別只轉動一次轉盤.小明同學先轉動轉盤,結果指針指向2,接下來小芳轉動轉盤,若把小明和小芳轉動轉盤指針指向的數字分別記作![]() 、
、![]() ,把
,把![]() 、
、![]() 作為點
作為點![]() 的橫、縱坐標.
的橫、縱坐標.

(1)寫出點![]() 所有可能的坐標;
所有可能的坐標;
(2)求點![]() 在直線
在直線![]() 上的概率.
上的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,邊長為 7 的正方形 OABC 放置在平面直角坐標系中,動點 P 從點 C 出發,以 每秒 1 個單位的速度向 O 運動,點 Q 從點 O 同時出發,以每秒 1 個單位的速度向點 A 運動,到達端點即停止運動,運動時間為 t 秒,連 PQ、BP、BQ.
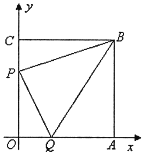
(1)寫出 B 點的坐標;
(2)填寫下表:
時間 t(單位:秒) | 1 | 2 | 3 | 4 | 5 | 6 |
OP 的長度 | ||||||
OQ 的長度 | ||||||
PQ 的長度 | ||||||
四邊形 OPBQ 的面積 |
①根據你所填數據,請描述線段 PQ 的長度的變化規律?并猜測 PQ 長度的最小值.
②根據你所填數據,請問四邊形 OPBQ 的面積是否會發生變化?并證明你的論斷;
(3)設點 M、N 分別是 BP、BQ 的中點,寫出點 M,N 的坐標,是否存在經過 M, N 兩點的反比例函數?如果存在,求出 t 的值;如果不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某農戶承包荒山若干畝,種果樹2000棵.今年水果總產量為18000千克,此水果在市場上每千克售![]() 元,在果園每千克售
元,在果園每千克售![]() 元
元![]() .該農戶將水果拉到市場出售平均每天出售1000千克,需8人幫忙,每人每天付工資25元,農用車運費及其他各項稅費平均每天100元.
.該農戶將水果拉到市場出售平均每天出售1000千克,需8人幫忙,每人每天付工資25元,農用車運費及其他各項稅費平均每天100元.
(1)分別用![]() 表示兩種方式出售水果的收入.
表示兩種方式出售水果的收入.
(2)若![]() 元,
元,![]() 元,且兩種方式都在相同的時間內售完全部水果,請你通過計算說明選擇哪種出售方式較好.
元,且兩種方式都在相同的時間內售完全部水果,請你通過計算說明選擇哪種出售方式較好.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB為⊙O的直徑,C、D兩點均在⊙O上,過點C作CE⊥AD于點E,且AC平分∠BAD.
(1)求證:CE為⊙O的切線;
(2)連結BD交AC于點F,若CF=5,sin∠CAD=![]() ,求線段BD的長.
,求線段BD的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個袋中均有三張除所標數值外完全相同的卡片,甲袋中的三張卡片上所標的數值分別為-7,-1,3,乙袋中的三張卡片上所標的數值分別為-2,1,6.先從甲袋中隨機取出一張卡片,用x表示取出的卡片上標的數值,再從乙袋中隨機取出一張卡片,用y表示取出的卡片上標的數值,把x、y分別作為點A的橫坐標、縱坐標.
(1)用適當的方法寫出點A(x,y)的所有情況;
(2)求點A落在第三象限的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形![]() 中,
中,![]() ,連接
,連接![]() ,以對角線
,以對角線![]() 為邊按逆時針方向作矩形
為邊按逆時針方向作矩形![]() ,使矩形
,使矩形![]() 矩形
矩形![]() ;再連接
;再連接![]() ,以對角線
,以對角線![]() 為邊,按逆時針方向作矩形,使矩形
為邊,按逆時針方向作矩形,使矩形![]() 矩形
矩形![]() , ..按照此規律作下去,若矩形
, ..按照此規律作下去,若矩形![]() 的面積記作
的面積記作![]() ,矩形
,矩形![]() 的面積記作
的面積記作![]() ,矩形
,矩形![]() 的面積記作
的面積記作![]() , ... 則
, ... 則![]() 的值為__________.
的值為__________.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com