Question

把一副三角板如圖(1)放置，其中∠ACB=∠DEC=90°，∠A=45°，∠D=30°，斜邊AB=12cm，DC=14cm，把三角板DCE繞點C逆時針旋轉(zhuǎn)15°得到△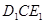（如圖2）．這時AB與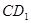相交于點O，與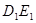相交于點F．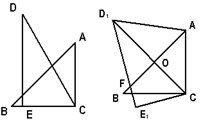

（1）填空：∠=     °；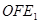
（2）請求出△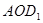的內(nèi)切圓半徑；
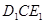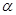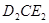（3）把△繞著點C逆時針再旋轉(zhuǎn)度（）得△，若△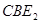為等腰三角形，求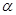的度數(shù)（精確到0.1°）．

Answer 1

（1）120°；（2）2；（3）37.7°、50.6°

解析試題分析：（1）根據(jù)旋轉(zhuǎn)的性質(zhì)結(jié)合三角板中的特殊角即可求得結(jié)果；
（2）由圖可得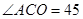度，即可得到AO=6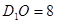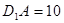，，，根據(jù)勾股定理的逆定理可證得△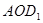為直角三角形，再根據(jù)直角三角形的性質(zhì)即可求得結(jié)果；
（3）根據(jù)等腰三角形的性質(zhì)分CB為底邊與CB為腰兩種情況分析即可.
（1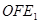）∠=120°；
（2）由題意得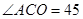度，AO=6，，
∵
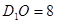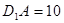
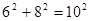
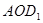∴△為直角三角形
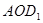∴△的內(nèi)切圓半徑；
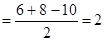（3）由題意當CB為底邊時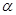，的度數(shù)為37.7°；當CB為腰時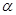，的度數(shù)為50.6°.
考點：勾股定理，旋轉(zhuǎn)的性質(zhì)
點評：能熟練應用勾股定理，利用旋轉(zhuǎn)前后的兩個圖形完全相等是解題關(guān)鍵．