
【題目】把一條12個單位長度的線段分成三條線段,其中一條線段成為4個單位長度,另兩條線段長都是單位長度的整數倍.
(1)不同分段得到的三條線段能組成多少個不全等的三角形?用直尺和圓規作這些三角形(用給定的單位長度,不寫作法,保留作圖痕跡);
(2)求出(1)中所作三角形外接圓的周長.
【答案】(1)2;(2)作圖見解析.
【解析】試題分析:(1)用列舉法得出所有不同分法的分法,根據三角形三邊關系得出能組成不全等的三角形的個數,應用尺規作圖.
(2)由勾股定理逆定理知,3,4,5構成三角形是直角三角形,根據直角三角形斜邊上中線等于斜邊 一半的性質,知3,4,5構成三角形的外接圓直徑等于5,從而根據周長公式求解;對4,4,4構成三角形是等邊三角形,根據銳角三角函數定義和特殊角的三角函數值求解即可.
試題解析:(1)∵把一條12個單位長度的線段分成三條線段,其中一條線段長為4個單位長度,另兩條線段長都是單位長度的整數倍,
∴不同分法的分法有:1,4,7;2,4,6;3,4,5;4,4,4.
∴能組成2個不全等的三角形:3,4,5;4,4,4.
作圖如下:
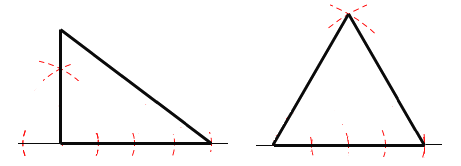
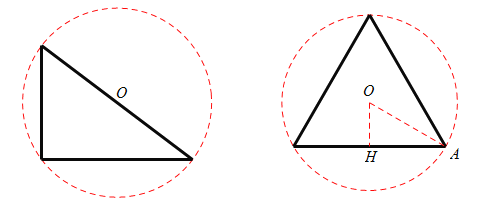
(2)對于3,4,5構成的三角形,由勾股定理逆定理知,它是直角三角形,所以它的外接圓直徑等于5.
∴它的三角形外接圓的周長為![]() .
.
對于4,4,4構成的三角形,如圖,知AH=2,∠OAH=30°,所以它的外接圓半徑等于![]() .
.
∴它的三角形外接圓的周長為![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,已知MB=ND,∠MBA=∠NDC,下列條件中不能判定△ABM≌△CDN的是( )
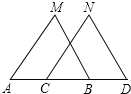
A.∠M=∠N B.AM=CN C.AB=CD D.AM∥CN
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正比例函數y=(m+2)x中,y的值隨x的增大而增大,而正比例函數y=(2m-3)x , y的值隨x的增大而減小,且m為整數,你能求出嗎?為什么?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場銷售一批名牌襯衫,平均每天可售出20件,每件盈利45元,為了擴大銷售.增加盈利,盡快減少庫存,商場決定采取適當的降價措施,經調查發現,如果每件襯衫每降價1元,商場平均每天可多售出4件,若商場平均每天盈利2100元,每件襯衫應降價多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.全等的兩個圖形成中心對稱
B.成中心對稱的兩個圖形必須重合
C.成中心對稱的兩個圖形全等
D.旋轉后能夠重合的兩個圖形成中心對稱
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com