
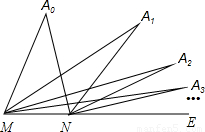
 α,
α, α,
α,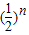 α,
α, α+
α+ α+
α+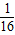 α+…+
α+…+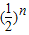 α=
α=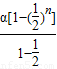 =2α[1-
=2α[1-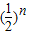 ].
].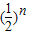 ].
].

科目:初中數學 來源: 題型:
 (2012•新化縣二模)一條排水管的截面如圖所示.已知排水管的截面圓半徑OB=100cm,截面圓圓心O到水面的距離OC是60cm,則水面寬AB=
(2012•新化縣二模)一條排水管的截面如圖所示.已知排水管的截面圓半徑OB=100cm,截面圓圓心O到水面的距離OC是60cm,則水面寬AB=查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•荊州模擬)某工藝品由一個底面朝上的圓錐體上方嵌入一圓球組成,其橫截面如圖所示,已知圓錐的母線AB、AC和球體相切,且與底座夾角均為75°,圓錐體底面的周長為20πcm,求球體的半徑(參考數據:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,結果精確到0.1)
(2012•荊州模擬)某工藝品由一個底面朝上的圓錐體上方嵌入一圓球組成,其橫截面如圖所示,已知圓錐的母線AB、AC和球體相切,且與底座夾角均為75°,圓錐體底面的周長為20πcm,求球體的半徑(參考數據:sin15°≈0.26,cos15°≈0.97,tan15°≈0.27,結果精確到0.1)查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com