
如圖,點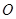 是等邊
是等邊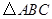 內一點,
內一點,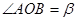 ,
, 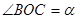 .將
.將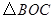 繞點
繞點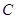 按順時針方向旋轉
按順時針方向旋轉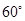 得
得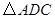 ,連接
,連接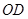 .
.
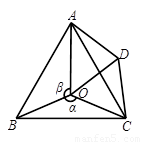
(1)當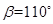 ,
,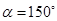 時,試判斷
時,試判斷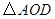 的形狀,并說明理由.
的形狀,并說明理由.
(2)請寫出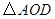 是等邊三角形時
是等邊三角形時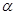 、
、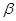 的度數.
的度數.
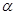 = 度;
= 度;
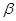 = 度.
= 度.
(3)探究:若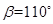 ,則
,則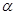 為多少度時,
為多少度時,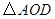 是等腰三角形?
是等腰三角形?
(只要寫出探究結果)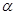 = ;
= ;
(1)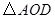 是直角三角形.(2)
是直角三角形.(2)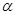 = 120 度;
= 120 度;
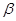 =
120 度.
=
120 度.
(3)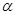 =
= 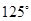 或
或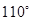 或
或 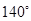
【解析】
試題分析:(1)
結論: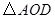 是直角三角形,
是直角三角形,
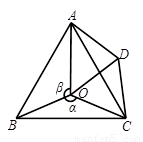
證明:由題意可得:△ACD≌△BCO,
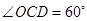 ,
,
∴CO=CD,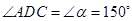 ,
,
∴△OCD是等邊三角形,
∴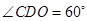 ,
,
∴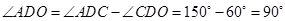 ,
,
∴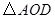 是直角三角形.
是直角三角形.
(2)由題意可得:△ACD≌△BCO, 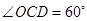 ,
,
∴CO=CD,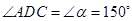 ,
,
∴△OCD是等邊三角形,
∴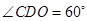
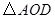 是等邊三角形,所以
是等邊三角形,所以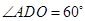
因此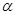 =
=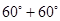 = 120 度;
= 120 度;
因為三角形AOD、COD都是等邊三角形,所以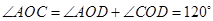
而 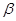 =
=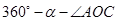 =
120 度.
=
120 度.
(3)
由(1)知△OCD是等邊三角形,那么OC=OD=CD,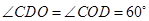 ;若
;若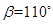
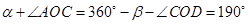 ;根據旋轉的特征
;根據旋轉的特征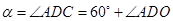 ;在三角形AOD中,根據三角形內角和定理
;在三角形AOD中,根據三角形內角和定理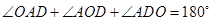 ,那么
,那么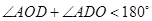 ,要使
,要使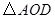 是等腰三角形,所以
是等腰三角形,所以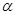 =
= 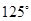 或
或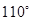 或
或  ;
;
考點:旋轉,等邊三角形
點評:本題考查平等邊三角形和旋轉,熟悉等邊三角形的性質和旋轉的概念和特征是解本題的關鍵


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
如圖,點![]() 是等邊
是等邊![]() 內一點,
內一點,![]() .將
.將![]() 繞點
繞點![]() 按順時針方向旋轉
按順時針方向旋轉![]() 得
得![]() ,連接
,連接![]()
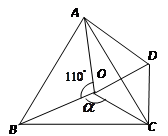
1.求證: ![]() 是等邊三角形;
是等邊三角形;
2.當![]() 時,試判斷
時,試判斷![]() 的形狀,并說明理由
的形狀,并說明理由
3.探究:當![]() 為多少度時,
為多少度時,![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中數學 來源: 題型:
如圖,點是等邊
內一點,
,
.將
繞點
按順時針方向旋轉
得
,連接
.

(1)當,
時,試判斷
的形狀,并說明理由。
(2)探究:若,那么
為多少度,
是等腰三角形?
(只要寫出探究結果)= 。
(3)請寫出是等邊三角形時
、
的度數。
= 度;
= 度。
查看答案和解析>>
科目:初中數學 來源: 題型:
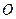 是等邊
是等邊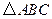 內一點,
內一點,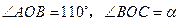 .將
.將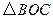 繞點
繞點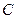 按順時針方向旋轉
按順時針方向旋轉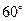 得
得 ,連接
,連接
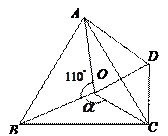
 是等邊三角形;
是等邊三角形;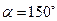 時,試判斷
時,試判斷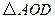 的形狀,并說明理由
的形狀,并說明理由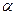 為多少度時,
為多少度時,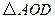 是等腰三角形?
是等腰三角形?查看答案和解析>>
科目:初中數學 來源:2012屆河南大學附中九年級上學期期中考試數學試卷 題型:解答題
如圖,點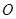 是等邊
是等邊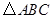 內一點,
內一點,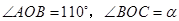 .將
.將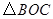 繞點
繞點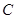 按順時針方向旋轉
按順時針方向旋轉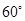 得
得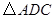 ,連接
,連接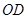

1.求證: 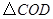 是等邊三角形;
是等邊三角形;
2.當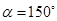 時,試判斷
時,試判斷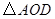 的形狀,并說明理由
的形狀,并說明理由
3.探究:當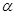 為多少度時,
為多少度時,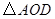 是等腰三角形?
是等腰三角形?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com