
深化理解(本小題滿分9分)
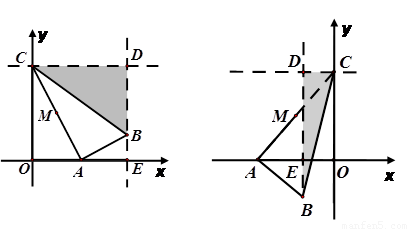
如圖,在平面直角坐標系中,點C的坐標為(0,4),A是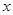 軸上的一個動點,M是線段AC的中點.把線段AM進行以A為旋轉中心、向順時針方向旋轉90°的旋轉變換得到AB.過B作
軸上的一個動點,M是線段AC的中點.把線段AM進行以A為旋轉中心、向順時針方向旋轉90°的旋轉變換得到AB.過B作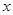 軸的垂線、過點C作
軸的垂線、過點C作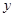 軸的垂線,兩直線交于點D,直線DB交
軸的垂線,兩直線交于點D,直線DB交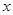 軸于一點E.
軸于一點E.
設A點的橫坐標為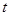 ,
,
(1)若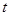 =3,則點B的坐標為
▲ ,若
=3,則點B的坐標為
▲ ,若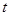 =-3,,則點B的坐標為 ▲ ;
=-3,,則點B的坐標為 ▲ ;
(2)若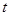 >0,△BCD的面積為
>0,△BCD的面積為 ,則
,則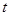 為何值時,
為何值時,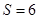 ?
?
(3)是否存在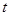 ,使得以B、C、D為頂點的三角形與△AOC相似?若存在,求此時
,使得以B、C、D為頂點的三角形與△AOC相似?若存在,求此時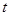 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(1)(5, 1.5 ) , (-1, -1.5 );(2)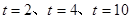 (3)
(3)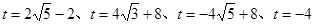 ,理由見解析
,理由見解析
【解析】(1)(5, 1.5 ) , (-1, -1.5 );
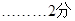
(2)①當 時,如圖(1)
時,如圖(1)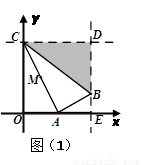
△AOC∽△BEA且相識比為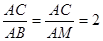
求得點B的坐標為(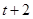 ,
,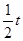 )
) 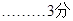
∴
解得 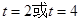
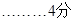
②當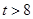 時,如圖(2)
時,如圖(2)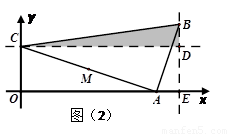
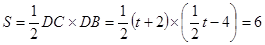
解得 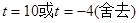
∴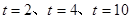
(3)①當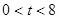 時,如圖(1)
時,如圖(1)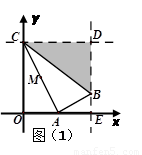
若△AOC∽△CDB
∴ 即:
即:
∴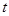 無解
無解
若△AOC∽△BDC,同理,解得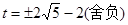
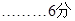
②當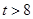 時,如圖(2)
時,如圖(2)
若△AOC∽△CDB,
∴ 即:
即: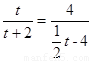
解得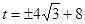 ,取
,取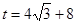
若△AOC∽△BDC,同理,解得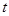 無解
無解
③當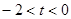 時,如圖(3)
時,如圖(3)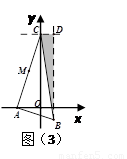
若△AOC∽△CDB
∴ 即:
即: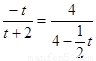
解得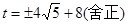
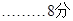
若△AOC∽△BDC,同理,解得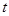 無解
無解
④當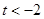 時,如圖(4)
時,如圖(4)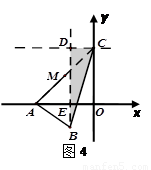
若△AOC∽△CDB
∴ 即:
即: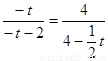
∴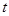 無解
無解
若△AOC∽△BDC,同理,解得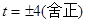
∴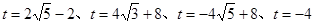
(1)根據勾股定理和對稱性求解
(2)求△BCD的面積時,可以CD為底、BD為高來解,那么表示出BD的長是關鍵;
Rt△CAO∽Rt△ABE,且知道AC、AB的比例關系,即可通過相似三角形的對應邊成比例求出BE的長,進一步得到BD的長,在表達BD長時,應分兩種情況考慮:①B在線段DE上,②B在ED的延長線上.
(3)通過B點所在的不同位置,分四種情況解答


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源:2012屆江蘇揚中市九年級下學期期中考試數學試卷(帶解析) 題型:解答題
深化理解(本小題滿分9分)
如圖,在平面直角坐標系中,點C的坐標為(0,4),A是 軸上的一個動點,M是線段AC的中點.把線段AM進行以A為旋轉中心、向順時針方向旋轉90°的旋轉變換得到AB.過B作
軸上的一個動點,M是線段AC的中點.把線段AM進行以A為旋轉中心、向順時針方向旋轉90°的旋轉變換得到AB.過B作 軸的垂線、過點C作
軸的垂線、過點C作 軸的垂線,兩直線交于點D,直線DB交
軸的垂線,兩直線交于點D,直線DB交 軸于一點E.
軸于一點E.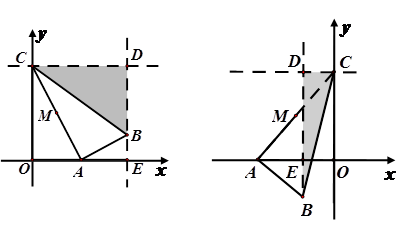
設A點的橫坐標為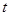 ,
,
(1)若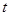 =3,則點B的坐標為 ▲ ,若
=3,則點B的坐標為 ▲ ,若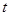 =-3,,則點B的坐標為 ▲ ;
=-3,,則點B的坐標為 ▲ ;
(2)若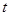 >0,△BCD的面積為
>0,△BCD的面積為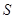 ,則
,則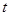 為何值時,
為何值時,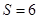 ?
?
(3)是否存在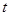 ,使得以B、C、D為頂點的三角形與△AOC相似?若存在,求此時
,使得以B、C、D為頂點的三角形與△AOC相似?若存在,求此時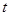 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com