
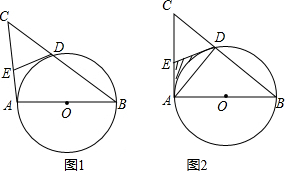
 已知:AB是⊙O的直徑,點C是⊙O外的一點,點E是AC上一點,AB=2.
已知:AB是⊙O的直徑,點C是⊙O外的一點,點E是AC上一點,AB=2.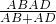 的值;②求陰影部分的面積.
的值;②求陰影部分的面積.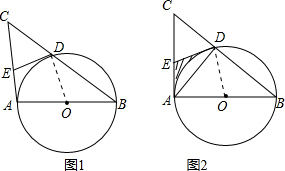 解:(1)如圖所示,
解:(1)如圖所示,
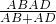 =
=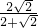 =
=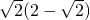 =2
=2 -2
-2 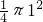 =
= 平方單位
平方單位 平方單位.
平方單位.

 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•欽州)如圖,某大樓的頂部樹有一塊廣告牌CD,小李在山坡的坡腳A處測得廣告牌底部D的仰角為60°.沿坡面AB向上走到B處測得廣告牌頂部C的仰角為45°,已知山坡AB的坡度i=1:
(2013•欽州)如圖,某大樓的頂部樹有一塊廣告牌CD,小李在山坡的坡腳A處測得廣告牌底部D的仰角為60°.沿坡面AB向上走到B處測得廣告牌頂部C的仰角為45°,已知山坡AB的坡度i=1:| 3 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,在平面直角坐標系中,直y=
如圖,在平面直角坐標系中,直y=| 3 |
| 2 |
| 16 |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
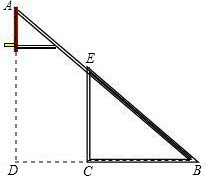
 紅星中學籃球課外活動小組的同學自己動手制作一副簡易籃球架.如圖,是籃球架的側面示意圖,已知籃板所在直線AD和直桿EC都與BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜桿AB與直桿EC的長分別是多少米?(計算結果精確到0.01米,參考數據:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)
紅星中學籃球課外活動小組的同學自己動手制作一副簡易籃球架.如圖,是籃球架的側面示意圖,已知籃板所在直線AD和直桿EC都與BC垂直,BC=2.8米,CD=1.8米,∠ABD=40°,求斜桿AB與直桿EC的長分別是多少米?(計算結果精確到0.01米,參考數據:(sin40°≈0.588,cos40°≈0.809,tan40°≈0.727.)查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com