【答案】
分析:(1)第一項先利用特殊角的三角函數值求出tan60°的值,然后判斷2-

為正數,利用絕對值的代數意義:正數的絕對值等于它本身化簡,第二項根據零指數公式化簡,第三項利用負指數公式化簡,最后一項先將二次根式化為最簡二次根式,約分得到結果,然后將各自的結果相加即可得到最后結果;
(2)將括號中第一項的分母分解因式,找出兩分式的最簡公分母,通分并利用同分母分式的減法法則計算,分子合并,同時利用除以一個數等于乘以這個數的倒數將除法運算化為乘法運算,約分后得到最簡結果,然后將a的值代入化簡后的式子中,即可得到原式的值;
(3)找出分式方程的最簡公分母,方程左右兩邊同時乘以最簡公分母,去分母后再利用去括號法則去括號,移項合并,將x的系數化為1,求出x的值,將求出的x的值代入最簡公分母中進行檢驗,即可得到原分式方程的解;
(4)移項并將x的系數化為求出不等式①的解集,去分母后移項并將x系數化為1求出不等式②的解集,找出兩解集的公共部分即可得到原不等式組的解集.
解答:解:(1)|2-tan60°|-(π-3.14)
+(-

)
-2+


=|2-
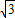
|-1+4+

×2

=2-

-1+4+

=5;
(2)(

-

)÷

=[

-

]•

=

•

=

•

=

,
當a=

-1時,原式=

=

;
(3)3-

=

,
去分母得:3(6x-2)-2=4,
18x-6-2=4,
解得:x=

經檢驗,x=

是原分式方程的解;
(4)

,
由不等式①,解得:x≤3,
由不等式②,去分母得:3x-3-4x+2>6,解得:x<-7,
在數軸上表示為下圖:

則原不等式組解集是x<-7.
點評:此題考查了分式的化簡求值,實數的混合運算,分式方程的解,以及一元一次不等式組的解法,分式的加減運算關鍵是通分,通分的關鍵是找出最簡公分母;分式的乘除運算關鍵是約分,約分的關鍵是找公因式,同時注意化簡求值題要將原式化為最簡后再代值.實數的混合運算涉及的知識有:a
=1(a≠0),a
-p=

(a≠0),以及二次根式的化簡,分式方程注意要檢驗,一元一次不等式組注意運用數形結合的思想,借助數軸找解集.

 )-2+
)-2+
 ;
; -
- )÷
)÷ ,其中a=
,其中a= -1.
-1. =
= ;
; ,并把解集在數軸上表示出來.
,并把解集在數軸上表示出來. 為正數,利用絕對值的代數意義:正數的絕對值等于它本身化簡,第二項根據零指數公式化簡,第三項利用負指數公式化簡,最后一項先將二次根式化為最簡二次根式,約分得到結果,然后將各自的結果相加即可得到最后結果;
為正數,利用絕對值的代數意義:正數的絕對值等于它本身化簡,第二項根據零指數公式化簡,第三項利用負指數公式化簡,最后一項先將二次根式化為最簡二次根式,約分得到結果,然后將各自的結果相加即可得到最后結果; )-2+
)-2+

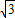 |-1+4+
|-1+4+ ×2
×2
 -1+4+
-1+4+
 -
- )÷
)÷
 -
- ]•
]•
 •
•
 •
•
 ,
, -1時,原式=
-1時,原式= =
= ;
; =
= ,
,
 是原分式方程的解;
是原分式方程的解; ,
,
 (a≠0),以及二次根式的化簡,分式方程注意要檢驗,一元一次不等式組注意運用數形結合的思想,借助數軸找解集.
(a≠0),以及二次根式的化簡,分式方程注意要檢驗,一元一次不等式組注意運用數形結合的思想,借助數軸找解集. 

 如圖所示,△ABC內接于⊙O,AB是直徑,D是
如圖所示,△ABC內接于⊙O,AB是直徑,D是

 sin60°•tan45°;
sin60°•tan45°;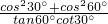 +tan60°;
+tan60°;