
【題目】(1)如圖1,在五邊形ABCDE中,AB=AE,∠B=∠BAE=∠AED=90°,∠CAD=45°,試猜想BC,CD,DE之間的數量關系.小明經過仔細思考,得到如下解題思路:
將△ABC繞點A逆時針旋轉90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即點D,E,F三點共線,易證△ACD≌ ,故BC,CD,DE之間的數量關系是 ;
(2)如圖2,在四邊形ABCD中,AB=AD,∠ABC+∠D=180°,點E,F分別在邊CB,DC的延長線上,∠EAF=![]() ∠BAD,連接EF,試猜想EF,BE,DF之間的數量關系,并給出證明.
∠BAD,連接EF,試猜想EF,BE,DF之間的數量關系,并給出證明.
(3)如圖3,在△ABC中,∠BAC=90°,AB=AC,點D,E均在邊BC上,且∠DAE=45°,若BD=2,CE=3,則DE的長為 .
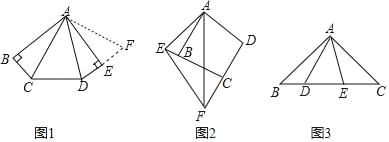
【答案】(1)△AFD,CD=DE+BC;(2EF=DF﹣BE,理由見解析;(3)![]() .
.
【解析】
(1)如圖1,將△ABC繞點A逆時針旋轉90°至△AEF,由∠B=∠AED=90°,得∠DEF=180°,即點D,E,F三點共線,易證△ACD≌△AFD,可得結論;
(2)如圖2,將△ABE繞點A逆時針旋轉,使AB與AD重合,得到△ADE',證明△AFE≌△AFE',據全等三角形的性質解答;
(3)將△ABD繞點A逆時針旋轉至△ACD',使AB與AC重合,連接ED',根據全等三角形的性質、勾股定理計算.
(1)BC,CD,DE之間的數量關系為:DF=DE+BC,理由是:
如圖1,將△ABC繞點A逆時針旋轉90°至△AEF,
由∠B=∠AED=∠AEF=90°,得∠DEF=180°,即點D,E,F三點共線,
∵∠BAE=90°,∠CAD=45°,
∴∠BAC+∠DAE=∠DAE+∠EAF=45°,
∴∠CAD=∠FAD,
∵AD=AD,
∴△ACD≌△FAD(SAS),
∴CD=DF=DE+EF=DE+BC,
故答案為:△AFD,CD=DE+BC;
(2)如圖2,EF,BE,DF之間的數量關系是EF=DF﹣BE.
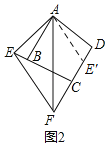
證明:將△ABE繞點A逆時針旋轉,使AB與AD重合,得到△ADE',
則△ABE≌△ADE',
∴∠DAE'=∠BAE,AE'=AE,DE'=BE,∠ADE'=∠ABE,
∴∠EAE'=∠BAD,
∵∠ABC+∠ADC=180°,∠ABC+∠ABE=180°,
∠ADE'=∠ADC,即E',D,F三點共線,
又∠EAF=![]() ∠BAD=
∠BAD=![]() ∠EAE'
∠EAE'
∴∠EAF=∠E'AF,
在△AEF和△AE'F中,
 ,
,
∴△AFE≌△AFE'(SAS),
∴FE=FE',
又∵FE'=DF﹣DE',
∴EF=DF﹣BE;
(3)如圖3,
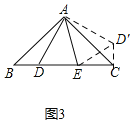
將△ABD繞點A逆時針旋轉至△ACD',使AB與AC重合,連接ED',則CD'=BD=2,
由(1)同理得,△AED≌AED',.
∴DE=D'E.
∵∠ACB=∠B=∠ACD'=45°,
∴∠ECD'=90°,
在Rt△ECD'中,ED'=![]() ,即DE=
,即DE=![]() ,
,
故答案為:![]() .
.


 名題金卷系列答案
名題金卷系列答案 優加精卷系列答案
優加精卷系列答案科目:初中數學 來源: 題型:
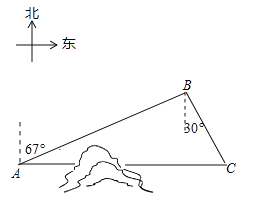
【題目】如圖,C地在A地的正東方向,因有大山阻隔,由A地到C地需繞行B地,已知B地位于A地北偏東67°方向,距離A地520km,C地位于B地南偏東30°方向,若打通穿山隧道,建成兩地直達高鐵,求A地到C地之間高鐵線路的長.(結果保留整數)
(參考數據:sin67°≈![]() ,cos67°≈
,cos67°≈![]() ,tan67°≈
,tan67°≈![]() ,
,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
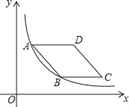
【題目】如圖,在平面直角坐標系中,菱形ABCD在第一象限內,邊BC與x軸平行,A、B兩點的縱坐標分別為3,1,反比例函數y=![]() 的圖象經過A,B兩點,則點D的坐標為( )
的圖象經過A,B兩點,則點D的坐標為( )
A. (2![]() ﹣1,3)B. (2
﹣1,3)B. (2![]() +1,3)
+1,3)
C. (2![]() ﹣1,3)D. (2
﹣1,3)D. (2![]() +1,3)
+1,3)
查看答案和解析>>
科目:初中數學 來源: 題型:
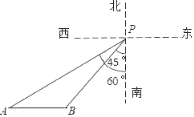
【題目】在某海域,一艘海監船在P處檢測到南偏西45°方向的B處有一艘不明船只,正沿正西方向航行,海監船立即沿南偏西60°方向以40海里/小時的速度去截獲不明船只,經過1.5小時,剛好在A處截獲不明船只,求不明船只的航行速度.(![]() ≈1.41,
≈1.41,![]() ≈1.73,結果保留一位小數).
≈1.73,結果保留一位小數).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某體育用品商店用4000元購進一批足球,全部售完后,又用3600元再次購進同樣的足球,但這次每個足球的進價是第一次進價的1.2倍,且數量比第一次少了10個.
(1)求第一次每個足球的進價是多少元?
(2)若第二次進貨后按150元/個的價格銷售,當售出10個后,根據市場情況,商店決定對剩余的足球全部按同一標準一次性打折售完,但要求這次的利潤不少于450元,問該商店最低可打幾折銷售?
查看答案和解析>>
科目:初中數學 來源: 題型:
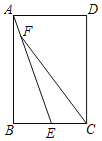
【題目】如圖,在矩形ABCD中,點E是BC上一點,連接AE,點F是AE上一點,連接FC,若∠BAE=∠EFC,CF=CD,AB:BC=3:2,AF=4,則FC的長為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
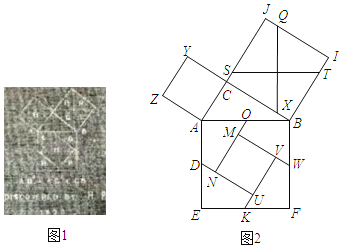
【題目】勾股定理有著悠久的歷史,它曾引起很多人的興趣.英國佩里加(H.Perigal,1801﹣1898)用“水車翼輪法”(圖1)證明了勾股定理.該證法是用線段QX,ST,將正方形BIJC分割成四個全等的四邊形,再將這四個四邊形和正方形ACYZ拼成大正方形AEFB(圖2).若AD=![]() ,tan∠AON=
,tan∠AON=![]() ,則正方形MNUV的周長為( )
,則正方形MNUV的周長為( )
A. ![]() B. 18C. 16D.
B. 18C. 16D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
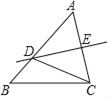
【題目】如圖,在△ABC中,AB=5,AC=4,∠A=60°,若邊AC的垂直平分線DE交AB于點D,連接CD,則△BDC的周長為( )
A. 8 B. 9 C. 5+![]() D. 5+
D. 5+![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com