
【題目】如圖,已知△ABC三個內角的平分線交于點O,點D在CA的延長線上,且DC=BC,AD=AO,若∠BAC=80°,則∠BCA的度數為 .

【答案】60°.
【解析】
試題可證明△COD≌△COB,得出∠D=∠CBO,再根據∠BAC=80°,得∠BAD=100°,由角平分線可得∠BAO=40°,從而得出∠DAO=140°,根據AD=AO,可得出∠D=20°,即可得出∠CBO=20°,則∠ABC=40°,最后算出∠BCA=60°
試題解析:∵△ABC三個內角的平分線交于點O,
∴∠ACO=∠BCO,
在△COD和△COB中,
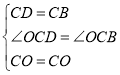 ,
,
∴△COD≌△COB,
∴∠D=∠CBO,
∵∠BAC=80°,
∴∠BAD=100°,
∴∠BAO=40°,
∴∠DAO=140°,
∵AD=AO,∴∠D=20°,
∴∠CBO=20°,
∴∠ABC=40°,
∴∠BCA=60°.


科目:初中數學 來源: 題型:
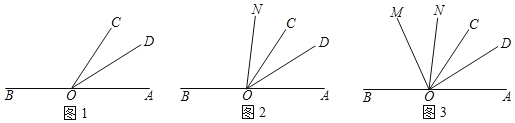
【題目】已知:點O為直線AB上一點,過點O作射線OC,使∠AOC=70°.
(1)如圖1,若OD平分∠AOC,求∠DOB的度數;
(2)射線OM從OA出發,繞點O以每秒6°的速度逆時針旋轉,同時,射線ON從OC出發繞點O以每秒4°的速度逆時針旋轉,OM與ON同時出發(當ON首次與OB重合時,兩條射線都停止運動),設運動的時間為t秒.
(i)如圖2,在整個運動過程中,當∠BON=2∠COM時,求t的值;
(ⅱ)如圖3,OP平分∠AOM,OQ平分∠BON,是否存在合適的t,使OC平分∠POQ,若存在,求出t的值,若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
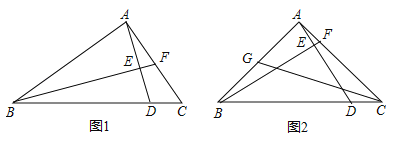
【題目】如圖,直角△ABC中,∠BAC=90°,D在BC上,連接AD,作BF⊥AD分別交AD于E,AC于F.
(1)如圖1,若BD=BA,求證:△ABE≌△DBE;
(2)如圖2,若BD=4DC,取AB的中點G,連接CG交AD于M,求證:①GM=2MC;②AG2=AFAC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,用棋子擺成的“上”字:

第一個“上”字 第二個“上”字 第三個“上”字
如果按照以上規律繼續擺下去,那么通過觀察,可以發現:
(1)第四、第五個“上”字分別需用 和 枚棋子.
(2)第n個“上”字需用 枚棋子.
(3)如果某一圖形共有102枚棋子,你知道它是第幾個“上”字嗎?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求證:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列圖形都是由同樣大小的圓按一定的規律組成,其中,第①個圖形中一共有2個圓:第②個圖形中一共有7個圓:第③個圖形中一共有16個圓;第④個圖形中一共有29個圓,…,則第⑦個圖形中圓的個數為_______.

查看答案和解析>>
科目:初中數學 來源: 題型:
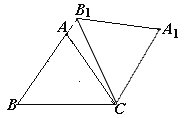
【題目】在△ABC中,AB=AC=5,cos∠ABC=![]() ,將△ABC繞點C順時針旋轉,得到△A1B1C.
,將△ABC繞點C順時針旋轉,得到△A1B1C.
(1)如圖①,當點B1在線段BA延長線上時.①求證:BB1∥CA1;②求△AB1C的面積;
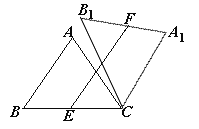
(2)如圖②,點E是BC邊的中點,點F為線段AB上的動點,在△ABC繞點C順時針旋轉過程中,點F的對應點是F1,求線段EF1長度的最大值與最小值的差.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知在紙面上有一數軸(如圖),折疊紙面.
![]()
(1)若1表示的點與![]() 表示的點重合,則
表示的點重合,則![]() 表示的點與數 表示的點重合;
表示的點與數 表示的點重合;
(2)若![]() 表示的點與3表示的點重合,回答以下問題:
表示的點與3表示的點重合,回答以下問題:
①5表示的點與數 表示的點重合;
②若數軸上![]() 、
、![]() 兩點之間的距離為9(
兩點之間的距離為9(![]() 在
在![]() 的左側),且
的左側),且![]() 、
、![]() 兩點經折疊后重合,求
兩點經折疊后重合,求![]() 、
、![]() 兩點表示的數是多少?
兩點表示的數是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com