
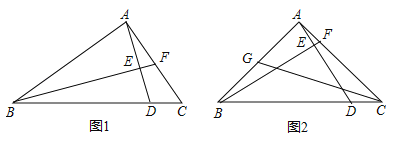
【題目】如圖,直角△ABC中,∠BAC=90°,D在BC上,連接AD,作BF⊥AD分別交AD于E,AC于F.
(1)如圖1,若BD=BA,求證:△ABE≌△DBE;
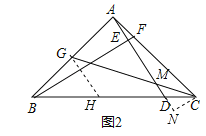
(2)如圖2,若BD=4DC,取AB的中點G,連接CG交AD于M,求證:①GM=2MC;②AG2=AFAC.
【答案】(1)證明見解析;(2)①證明見解析;②證明見解析.
【解析】
試題分析:(1)根據全等三角形的判定定理即可得到結論;
(2)①過G作GH∥AD交BC于H,由AG=BG,得到BH=DH,根據已知條件設DC=1,BD=4,得到BH=DH=2,根據平行線分線段成比例定理得到![]() ,求得GM=2MC;
,求得GM=2MC;
②過C作CN⊥AD交AD的延長線于N,則CN∥AG,根據相似三角形的性質得到![]() ,由①知GM=2MC,得到2NC=AG,根據相似三角形的性質得到
,由①知GM=2MC,得到2NC=AG,根據相似三角形的性質得到![]() ,等量代換得到
,等量代換得到![]() ,于是得到結論.
,于是得到結論.
試題解析:(1)在Rt△ABE和Rt△DBE中,∵BA=BD,BE=BE,∴△ABE≌△DBE;
(2)①過G作GH∥AD交BC于H,∵AG=BG,∴BH=DH,∵BD=4DC,設DC=1,BD=4,∴BH=DH=2,∵GH∥AD,∴![]() ,∴GM=2MC;
,∴GM=2MC;
②過C作CN⊥AC交AD的延長線于N,則CN∥AG,∴△AGM∽△NCM,∴![]() ,由①知GM=2MC,∴2NC=AG,∵∠BAC=∠AEB=90°,∴∠ABF=∠CAN=90°﹣∠BAE,∴△ACN∽△BAF,∴
,由①知GM=2MC,∴2NC=AG,∵∠BAC=∠AEB=90°,∴∠ABF=∠CAN=90°﹣∠BAE,∴△ACN∽△BAF,∴![]() ,∵AB=AG,∴
,∵AB=AG,∴![]() ,∴2CNAG=AFAC,∴AG2=AFAC.
,∴2CNAG=AFAC,∴AG2=AFAC.


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:初中數學 來源: 題型:
【題目】下列說法中正確的是( )
A.“任意畫出一個等邊三角形,它是軸對稱圖形”是隨機事件
B.“任意畫出一個平行四邊形,它是中心對稱圖形”是必然事件
C.“概率為0.0001的事件”是不可能事件
D.任意擲一枚質地均勻的硬幣10次,正面向上的一定是5次
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,規定:拋物線
中,規定:拋物線![]() 的伴隨直線為
的伴隨直線為![]() .例如:拋物線
.例如:拋物線![]() 的伴隨直線為
的伴隨直線為![]() ,即
,即![]()
(1)在上面規定下,拋物線![]() 的頂點為 .伴隨直線為 ;拋物線
的頂點為 .伴隨直線為 ;拋物線![]() 與其伴隨直線的交點坐標為 和 ;
與其伴隨直線的交點坐標為 和 ;
(2)如圖,頂點在第一象限的拋物線![]() 與其伴隨直線相交于點
與其伴隨直線相交于點![]() (點
(點![]() 在點
在點![]() 的右側)與
的右側)與![]() 軸交于點
軸交于點![]()
①若![]() 求
求![]() 的值;
的值;
②如果點![]() 是直線
是直線![]() 上方拋物線的一個動點,
上方拋物線的一個動點,![]() 的面積記為
的面積記為![]() ,當
,當![]() 取得最大值
取得最大值![]() 時,求
時,求![]() 的值.
的值.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形OABC的對角線OB,AC相交于點D,且BE∥AC,AE∥OB,
(1)求證:四邊形AEBD是菱形;
(2)如果OA=3,OC=2,求出經過點E的反比例函數解析式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市今年約有140000人報名參加初中學業水平考試,用科學記數法表示140000為( )
A.14×104
B.14×103
C.1.4×104
D.1.4×105
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知點P位于第二象限,距y軸3個單位長度,距x軸4個單位長度,則點P的坐標是( )
A. (-3,4)B. (3,-4)C. (4,-3)D. (-4,3)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=BC , ∠ABC=90°,F為AB延長線上一點,點E在BC上,且AE=CF . 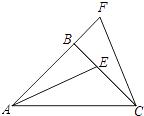
(1)求證:△ABE≌△CBF;
(2)若∠BAE=25°,求∠ACF的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
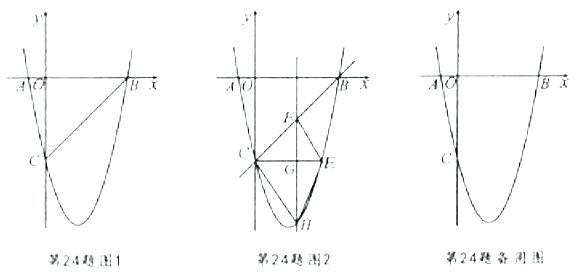
【題目】如圖1,在平面直角坐標系中,已知拋物線![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() .
.
(1)求拋物線的函數表達式;
(2)若點![]() 是
是![]() 軸上的一點,且以
軸上的一點,且以![]() 為頂點的三角形與
為頂點的三角形與![]() 相似,求點
相似,求點![]() 的坐標;
的坐標;
(3)如圖2,![]() 軸瑋拋物線相交于點
軸瑋拋物線相交于點![]() ,點
,點![]() 是直線
是直線![]() 下方拋物線上的動點,過點
下方拋物線上的動點,過點![]() 且與
且與![]() 軸平行的直線與
軸平行的直線與![]() ,
,![]() 分別交于點
分別交于點![]() ,
,![]() ,試探究當點
,試探究當點![]() 運動到何處時,四邊形
運動到何處時,四邊形![]() 的面積最大,求點
的面積最大,求點![]() 的坐標及最大面積;
的坐標及最大面積;
(4)若點![]() 為拋物線的頂點,點
為拋物線的頂點,點![]() 是該拋物線上的一點,在
是該拋物線上的一點,在![]() 軸,
軸,![]() 軸上分別找點
軸上分別找點![]() ,
,![]() ,使四邊形
,使四邊形![]() 的周長最小,求出點
的周長最小,求出點![]() ,
,![]() 的坐標.
的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com