
【題目】如圖,一次函數y=kx+b與反比例函數y=![]() 的圖象相較于A(2,3),B(﹣3,n)兩點.
的圖象相較于A(2,3),B(﹣3,n)兩點.
(1)求一次函數與反比例函數的解析式;
(2)根據所給條件,請直接寫出不等式kx+b>![]() 的解集;
的解集;
(3)過點B作BC⊥x軸,垂足為C,求S△ABC.

【答案】(1)反比例函數的解析式為:y=![]() ,一次函數的解析式為:y=x+1;
,一次函數的解析式為:y=x+1;
(2)﹣3<x<0或x>2;
(3)5.
【解析】
(1)根據點A位于反比例函數的圖象上,利用待定系數法求出反比例函數解析式,將點B坐標代入反比例函數解析式,求出n的值,進而求出一次函數解析式
(2)根據點A和點B的坐標及圖象特點,即可求出反比例函數值大于一次函數值時x的取值范圍
(3)由點A和點B的坐標求得三角形以BC 為底的高是10,從而求得三角形ABC 的面積
解:(1)∵點A(2,3)在y=![]() 的圖象上,∴m=6,
的圖象上,∴m=6,
∴反比例函數的解析式為:y=![]() ,
,
∴n=![]() =﹣2,
=﹣2,
∵A(2,3),B(﹣3,﹣2)兩點在y=kx+b上,
∴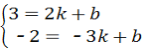 ,
,
解得:![]() ,
,
∴一次函數的解析式為:y=x+1;
(2)由圖象可知﹣3<x<0或x>2;
(3)以BC為底,則BC邊上的高為3+2=5,
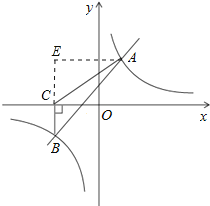
∴S△ABC=![]() ×2×5=5.
×2×5=5.


科目:初中數學 來源: 題型:
【題目】閱讀材料:各類方程的解法
求解一元一次方程,根據等式的基本性質,把方程轉化為x=a的形式.求解二元一次方程組,把它轉化為一元一次方程來解;類似的,求解三元一次方程組,把它轉化為解二元一次方程組.求解一元二次方程,把它轉化為兩個一元一次方程來解.求解分式方程,把它轉化為整式方程來解,由于“去分母”可能產生增根,所以解分式方程必須檢驗.各類方程的解法不盡相同,但是它們有一個共同的基本數學思想![]() 轉化,把未知轉化為已知.
轉化,把未知轉化為已知.
用“轉化”的數學思想,我們還可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通過因式分解把它轉化為x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)問題:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“轉化”思想求方程![]() 的解;
的解;
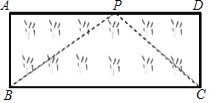
(3)應用:如圖,已知矩形草坪ABCD的長AD=8m,寬AB=3m,小華把一根長為10m的繩子的一端固定在點B,沿草坪邊沿BA,AD走到點P處,把長繩PB段拉直并固定在點P,然后沿草坪邊沿PD、DC走到點C處,把長繩剩下的一段拉直,長繩的另一端恰好落在點C.求AP的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,二次函數y=ax2+bx+c(a≠0)的頂點A(-3,0),與y軸交于點B(0,4),在第一象限內有一點P(m,n),且滿足4m+3n=12.
(1)求二次函數解析式.
(2)若以點P為圓心的圓與直線AB、x軸相切,求點P的坐標.
(3)若點A關于y軸的對稱點為點A′,點C在對稱軸上,且2∠CBA+∠PA′O=90.求點C的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】圖甲是小張同學設計的帶圖案的花邊作品,該作品由形如圖乙的矩形圖案設計拼接面成(不重疊,無縫隙).圖乙中,點E、F、G、H分別為矩形AB、BC、CD、DA的中點,若AB=4,BC=6,則圖乙中陰影部分的面積為
_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一面利用墻,用籬笆圍成的矩形花圃ABCD的面積為Sm2,垂直于墻的AB邊長為xm.

(1)若墻可利用的最大長度為8m,籬笆長為18m,花圃中間用一道籬笆隔成兩個小矩形.
①求S與x之間的函數關系式;
②如何圍矩形花圃ABCD的面積會最大,并求最大面積.
(2)若墻可利用最大長度為50m,籬笆長99m,中間用n道籬笆隔成(n+1)小矩形,當這些小矩形都是正方形且x為正整數時,請直接寫出所有滿足條件的x、n的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形OABC為平行四邊形,B、C在⊙O上,A在⊙O外,sin∠OCB=![]() .
.
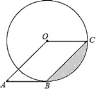
(1)求證:AB與⊙O相切;
(2)若BC=10cm,求圖中陰影部分的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為了了解今年九年級學生的數學學習情況,在中考考前適應性訓練測試后,對九年級全體同學的數學成績作了統計分析,按照成績高低分為A、B、C、D四個等級并繪制了如圖1和圖2的統計圖(均不完整),請結合圖中所給出的信息解答問題:
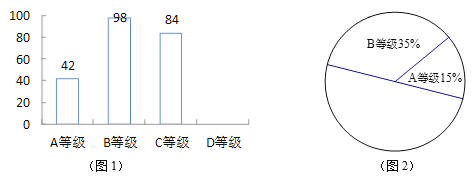
(1)該校九年級學生共有 人.
(2)補全條形統計圖與扇形統計圖.(要求:請將扇形統計圖的空白部分按比例分成兩部分.)
查看答案和解析>>
科目:初中數學 來源: 題型:
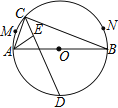
【題目】如圖,![]() 是
是![]() 的直徑,
的直徑,![]() 、
、![]() 是弧
是弧![]() (異于
(異于![]() 、
、![]() )上兩點,
)上兩點,![]() 是弧
是弧![]() 上一動點,
上一動點,![]() 的角平分線交
的角平分線交![]() 于點
于點![]() ,
,![]() 的平分線交
的平分線交![]() 于點
于點![]() .當點
.當點![]() 從點
從點![]() 運動到點
運動到點![]() 時,則
時,則![]() 、
、![]() 兩點的運動路徑長的比是( )
兩點的運動路徑長的比是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com