
【題目】已知拋物線y=![]() 的圖像與
的圖像與![]() 軸的一個交點為A(-1,0),另一個交點為B,與
軸的一個交點為A(-1,0),另一個交點為B,與![]() 軸交于點C(0,﹣3),頂點為D.
軸交于點C(0,﹣3),頂點為D.
(1)求二次函數的解析式和點D的坐標;
(2)若點M是拋物線在![]() 軸下方圖像上的一動點,過點M作MN∥
軸下方圖像上的一動點,過點M作MN∥![]() 軸交線段BC于點N,當MN取最大值時,點M 的坐標;
軸交線段BC于點N,當MN取最大值時,點M 的坐標;
(3)將該拋物線向上或向下平移,使得新拋物線的頂點D落在x軸上,原拋物線上一點P平移后的對應點為Q,如果∠OQP=∠OPQ,試求點Q的坐標.
【答案】(1)拋物線的解析式為y=x2﹣2x﹣3,頂點D(1,﹣4);(2)點M的坐標為(![]() ,
,![]() );(3)Q(
);(3)Q(![]() ,2)或(
,2)或(![]() ,2)
,2)
【解析】
(1)把點A(-1,0),C(0,﹣3)代入解析式求解,然后化為頂點式即可;
(2)由(1)的解析式求出函數與x軸的交點坐標,即可得到B(3,0),根據已知條件求出直線BC的解析式![]() ,根據M在二次函數的圖像上,N在一次函數圖像上,可設兩個點的坐標為M
,根據M在二次函數的圖像上,N在一次函數圖像上,可設兩個點的坐標為M ![]() ,N
,N![]() ,可得MN
,可得MN ![]() ,得到關于m的方程,化為頂點式即可得到結果;
,得到關于m的方程,化為頂點式即可得到結果;
(3)先根據頂點在x軸上確定函數平移的距離,再根據∠OQP=∠OPQ得到OP=OQ,即可得到結果.
解:(1)∵拋物線y=![]() 經過A(-1,0),C(0,﹣3);
經過A(-1,0),C(0,﹣3);
得![]() ;
;
∴![]() ;
;
∴拋物線的解析式為y=x2﹣2x﹣3;
∴y=(x﹣1)2﹣4;
∴頂點D(1,﹣4).
(2)∵y=x2﹣2x﹣3;
當 y=0時,x2﹣2x﹣3=0;
解得 ![]() ,
,![]() ;
;
∴B(3,0).
設直線BC解析式為y=kx+b(k≠0);
把B(3,0)、C(0,-3)代入y=kx+b;
可得![]() ;
;
解得:![]() ;
;
∴直線BC解析式為![]() ;
;
設M ![]() ,N
,N![]() ;
;
∴MN ![]()
![]()
![]() ;
;
∴當MN最大時,點M的坐標為(![]() ,
,![]() ).
).
(3)由(1)可得拋物線頂點坐標D(1,﹣4),根據題意可得拋物線向上平移4個單位長度;
∵點P在原拋物線y=x2﹣2x﹣3上;
∴設P(x, x2﹣2x﹣3),則Q(x, x2﹣2x+1);
∵∠OQP=∠OPQ;
∴OP=OQ;
∴得到![]() 或
或![]() ;
;
∴Q(![]() ,2)或(
,2)或(![]() ,2).
,2).


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
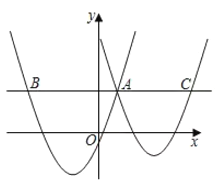
【題目】如圖,在平面直角坐標系中,拋物線![]() 與
與![]() 交于點A.過點A作
交于點A.過點A作![]() 軸的垂線,分別交兩條拋物線于點B、C(點B在點A左側,點C在點A右側),則線段BC的長為____.
軸的垂線,分別交兩條拋物線于點B、C(點B在點A左側,點C在點A右側),則線段BC的長為____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,E是邊AD上的一點,將△CDE沿CE折疊得到△CFE,點F恰好落在邊AB上.
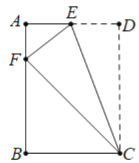
(1)證明:△AEF∽△BFC.
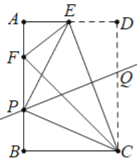
(2)若AB=![]() ,BC=1,作線段CE的中垂線,交AB于點P,交CD于點Q,連結PE,PC.
,BC=1,作線段CE的中垂線,交AB于點P,交CD于點Q,連結PE,PC.
①求線段DQ的長.
②試判斷△PCE的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明是一名健步走運動的愛好者,他用手機軟件記錄了他近期健步走的步數(單位:萬步),繪制出如下的統計圖①和統計圖②,請根據相關信息,解答下列問題:
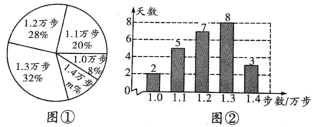
(Ⅰ)本次記錄的總天數為_____________,圖①中m的值為______________;
(Ⅱ)求小名近期健步走步數的平均數、眾數和中位數;
(Ⅲ)根據樣本數據,若小明堅持健步走一年(記為365天),試估計步數為1.1萬步的天數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知⊙O是△ABC的外接圓,AD是⊙O的直徑,且BD=BC,延長AD到E,且有∠EBD=∠CAB.
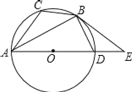
⑴求證:BE是⊙O的切線;
⑵若BC=![]() ,AC=5,求圓的直徑AD的長.
,AC=5,求圓的直徑AD的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
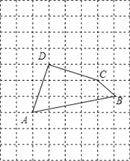
【題目】如圖,將四邊形ABCD放在每個小正方形的邊長為1的網格中,點A.B、C、D均落在格點上.
(Ⅰ)計算AD2+DC2+CB2的值等于_____;
(Ⅱ)請在如圖所示的網格中,用無刻度的直尺,畫出一個以AB為一邊的矩形,使該矩形的面積等于AD2+DC2+CB2,并簡要說明畫圖方法(不要求證明).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形 ABCD 中,AB=8,BC=6,將矩形 ABCD 繞點 A 逆時針旋轉得到矩形 AEFG,AE,FG 分別交射線CD 于點 PH,連結 AH,若 P 是 CH 的中點,則△APH 的周長為( )
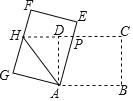
A. 15 B. 18 C. 20 D. 24
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,菱形![]() 中,對角線
中,對角線![]() 、
、![]() 相交于點
相交于點![]() ,
,![]() ,
,![]() ,動點
,動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以
以![]() 的速度向點
的速度向點![]() 運動,同時動點
運動,同時動點![]() 從點
從點![]() 出發,沿線段
出發,沿線段![]() 以
以![]() 支向點
支向點![]() 運動,當其中一個動點停止時另一個動點也隨之停止,設運動時間為
運動,當其中一個動點停止時另一個動點也隨之停止,設運動時間為![]() (單位:
(單位:![]() )(
)(![]() ),以點
),以點![]() 為圓心,
為圓心,![]() 長為半徑的⊙M與射線
長為半徑的⊙M與射線![]() 、線段
、線段![]() 分別交于點
分別交于點![]() 、
、![]() ,連接
,連接![]() .
.
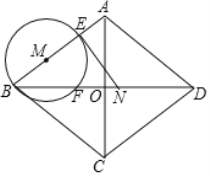
(1)求![]() 的長(用含有
的長(用含有![]() 的代數式表示),并求出
的代數式表示),并求出![]() 的取值范圍;
的取值范圍;
(2)當![]() 為何值時,線段
為何值時,線段![]() 與⊙M相切?
與⊙M相切?
(3)若⊙M與線段![]() 只有一個公共點,求
只有一個公共點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com