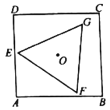
【題目】如圖，正方形
的邊長為4，在這個正方形內作等邊三角形
（三角形的頂點可以在正方形的邊上），使它們的中心重合，則
的頂點到正方形的頂點的最短距離是___________．
【答案】
【解析】
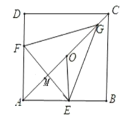
當G，O，C共線時，△EFG的頂點到正方形ABCD的頂點的最短，即點G在對角線上，在△AOE中，∠CAE=45°，∠AOE=60°，OE=r，解三角形可求r，即可求最短距離．
如圖：當G，O，C共線時，△EFG的頂點到正方形ABCD的頂點的最短，即點G在對角線上．
作EM⊥AC于M
∵ABCD是正方形，AB=4
∴AC=
，AO=
，∠CAB=45°
∵△EFG是等邊三角形
∴∠GOE=120°
∴∠AOE=60°
設OE為r
∵∠AOE=60°，ME⊥AO
∴MO=
OE=r，ME=
MO=
r
∵∠MAE=45°，AM⊥ME
∴∠MAE=∠MEA=45°，
∴AM=ME=r，
∵AM+MO=AO
∴r+r=
∴r=
∵AG=AM=MO+OG=r+r+r=
∴GC=
故答案為：．
智能訓練練測考系列答案
計算高手系列答案科目：初中數學 來源： 題型：
【題目】函數y=ax2+bx+c的圖像如圖所示，那么關于x的方程ax2+bx+c-4=0的根的情況是( )
A．有兩個不相等的實數根 B．有兩個異號的實數根
C．有兩個相等的實數根 D．沒有實數根
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】請從以下兩個小題中任選一個作答，若多選，則按所選的第一題計分．
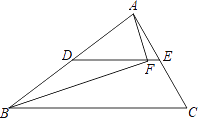
A．如圖，DE為△ABC的中位線，點F為DE上一點，且∠AFB=90°，若AB=8，BC=10，則EF的長為________．
B．小智同學在距大雁塔塔底水平距離為138米處，看塔頂的仰角為24.8（不考慮身高因素），則大雁塔市約為________米．（結果精確到0.1米）
查看答案和解析>>
科目：初中數學 來源： 題型：
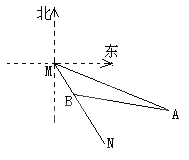
【題目】如圖所示,MN表示某飲水工程的一段設計路線,從M到N的走向為南偏東30°,在M的南偏東60°的方向上有一點A,以點A為圓心．以500m為半徑的圓形區域為居民區,取MN上另一點B,測得BA的方向為南偏東75°,已知MB=400m．通過計算回答,如果不改變方向,輸水路線是否會穿過該居民區?（
≈1．73）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】閱讀以下材料，并解決相應問題：
材料一：換元法是數學中的重要方法，利用換元法可以從形式上簡化式子，在求解某些特殊方程時，利用換元法常常可以達到轉化的目的，例如在求解一元四次方程
，就可以令
，則原方程就被換元成
，解得 t 1，即，從而得到原方程的解是 x 1
材料二：楊輝三角形是中國數學上一個偉大成就，在中國南宋數學家楊輝 1261 年所著的《詳解九章算法》一書中出現，它呈現了某些特定系數在三角形中的一種有規律的幾何排列，下圖為楊輝三角形：
……………………………………
（1）利用換元法解方程：
（2）在楊輝三角形中，按照自上而下、從左往右的順序觀察， an 表示第 n 行第 2 個數（其中 n≥4），bn 表示第 n 行第 3 個數，
表示第
行第 3 個數，請用換元法因式分解：
查看答案和解析>>
科目：初中數學 來源： 題型：
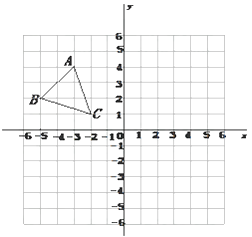
【題目】如圖，平面直角坐標系內，小正方形網格的邊長為1個單位長度，△ABC 的三個頂點的坐標分別 A（-3，4）B（-5，2）C（-2，1）
（1）畫出 △ABC關于y 軸的對稱圖形 △A1B1C1；
（2）畫出將△ABC 繞原點 O逆時針方向旋轉90°得到的△A2B2C2 ；
（3）求（2）中線段 OA掃過的圖形面積．
查看答案和解析>>
科目：初中數學 來源： 題型：
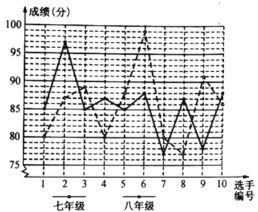
【題目】在倡導“社會主義核心價值觀”演講比賽中，某校根據初賽成績在七、八年級分別選出10名同學參加決賽，對這些同學的決賽成績進行整理分析，繪制成如下團體成績統計表和選手成績折線統計圖：
七年級 | 八年級 | |
平均數 | 85.7 | _______ |
眾數 | _______ | _______ |
方差 | 37.4 | 27.8 |
根據上述圖表提供的信息，解答下列問題：
（1）請你把上面的表格填寫完整；
（2）考慮平均數與方差，你認為哪個年級的團體成績更好？
（3）假設在每個年級的決賽選手中分別選出2個參加決賽，你認為哪個年級的實力更強一些？請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
