
【題目】(1)(發現)如圖①,已知等邊△ABC,將直角三角板的60°角頂點D任意放在BC邊上(點D不與點B、C重合),使兩邊分別交線段AB、AC于點E、F.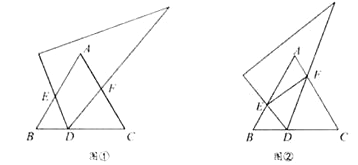
①若AB=6,AE=4,BD=2,則CF =________;
②求證:△EBD∽△DCF.
(2)(思考)若將圖①中的三角板的頂點D在BC邊上移動,保持三角板與邊AB、AC的兩個交點E、F都存在,連接EF,如圖②所示.問點D是否存在某一位置,使ED平分∠BEF且FD平分∠CFE?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
(3)(探索)如圖③,在等腰△ABC中,AB=AC,點O為BC邊的中點,將三角形透明紙板的一個頂點放在點O處(其中∠MON=∠B),使兩條邊分別交邊AB、AC于點E、F(點E、F均不與△ABC的頂點重合),連接EF.設∠B=α,則△AEF與△ABC的周長之比為________(用含α的表達式表示)
.
【答案】(1)①4;②證明見解析;(2)存在;(3)1-cosα.
【解析】(1)①先求出BE的長度后發現BE=BD,又∠B=60°,可知△BDE是等邊三角形,可得∠BDE=60°,另外∠EDF=60°,可證得△CDF是等邊三角形,從而CF=CD=BC-BD;
②證明△EBD∽△DCF,這個模型可稱為“一線三等角相似模型”,根據“AA”判定相似;
(2)【思考】由平分線可聯系到角平分線的性質“角平分線上的點到角兩邊的距離相等”,可過D作DM⊥BE,DG⊥EF,DN⊥CF,則DM=DG=DN,從而通過證明△BDM△CDN可得BD=CD;
(3)【探索】由已知不難求得C△ABC=AB+BC+CA=2AB+2OB=2(m+mcosα),則需要用m和α的三角函數表示出C△AEF,C△AEF=AE+EF+AF;題中直接已知O是BC的中點,應用(2)題的方法和結論,作OG⊥BE,OD⊥EF,OH⊥CF,可得EG=ED,FH=DF,則C△AEF=AE+EF+AF= AG+AH=2AG,而AG=AB-OB,從而可求得.
(1)①∵△ABC是等邊三角形,
∴AB=BC=AC=6,∠B=∠C=60°,
∵AE=4,
∴BE=2,則BE=BD,
∴△BDE是等邊三角形,
∴∠BDE=60°,
又∵∠EDF=60°,
∴∠CDF=180°-∠EDF-∠B=60°,則∠CDF =∠C=60°,
∴△CDF是等邊三角形,
∴CF=CD=BC-BD=6-2=4;
②證明:∵∠EDF=60°,∠B=60°
∴∠CDF+∠BDE=120°,∠BED+∠BDE=120°,
∴∠BED=∠CDF,
又∵∠B=∠C,
∴△EBD∽△DCF
(2)存在.如圖,作DM⊥BE,DG⊥EF,DN⊥CF,垂足分別為M,G,N,
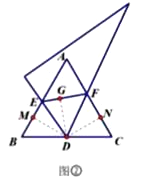
∵ED平分∠BEF且FD平分∠CFE,
∴DM=DG=DN,
又∵∠B=∠C=60°,∠BMD=∠CND=90°,
∴△BDM△CDN,
∴BD=CD,
即點D是BC的中點,
∴![]() ;
;
( 3 )連結AO,作OG⊥BE,OD⊥EF,OH⊥CF,垂足分別為G,D,H,
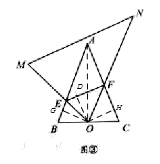
則∠BGO=∠CHO=90°,
∵AB=AC,O是BC的中點
∴∠B=∠C,OB=OC,
∴△OBG△OCH,
∴OG=OH,GB=CH,∠BOG=∠COH=90°α,
則∠GOH=180°-(∠BOG+∠COH)=2α,
∵∠EOF=∠B=α,
則∠GOH=2∠EOF=2α,
由(2)題可猜想應用EF=ED+DF=EG+FH,
則 C△AEF=AE+EF+AF=AE+EG+FH+AF=AG+AH=2AG,
設AB=m,則OB=mcosα,GB=mcos2α,
![]() .
.


科目:初中數學 來源: 題型:
【題目】“龜兔首次賽跑”之后,輸了比賽的兔子沒有氣餒,總結反思后,和烏龜約定再賽一場.圖中的函數圖象刻畫了“龜兔再次賽跑”的故事(x表示烏龜從起點出發所行的時間,y1表示烏龜所行的路程,y2表示兔子所行的路程).有下列說法:
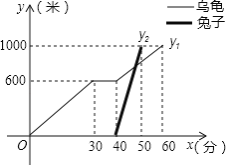
①“龜兔再次賽跑”的路程為1000米;
②兔子和烏龜同時從起點出發;
③烏龜在途中休息了10分鐘;
④兔子在途中750米處追上烏龜.
其中正確的說法是 .(把你認為正確說法的序號都填上)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一只跳蚤在第一象限及x軸、y軸上跳動,第一秒它從原點跳動到點(0,1),第二秒它從點(0,1)跳到點(1,1),然后接著按圖中箭頭所示方向跳動[即(0,0)→(0,1)→(1,1)→(1,0)→…],每秒跳動一個單位長度,那么30秒后跳蚤所在位置的坐標是___.
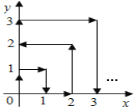
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,長方體的長為15寬為10,高為20,點B離點C的距離為5,一只螞蟻如果要沿著長方體的表面從點A爬到點B,需要爬行的最短距離是( )

A. 20 B. 25 C. 30 D. 32
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD⊥BC,AE平分∠BAC
(1)若∠B=70°,∠C=30°,求;
①∠BAE的度數.
②∠DAE的度數.
(2)探究:如果只知道∠B=∠C+40°,那么能求岀∠DAE的度數嗎?若能,請你寫出求解過程;若不能,請說明理由.
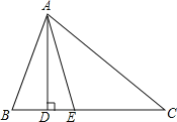
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在數學課本中,有這樣一道題:已知:如(圖1),∠B+∠C=∠BEC求證:AB∥CD
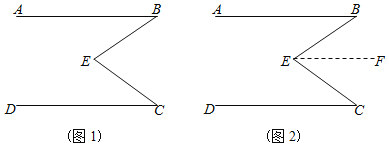
(1)請補充下面證明過程
證明:過點E,做EF∥AB,如(圖2)
∴∠B=∠
∵∠B+∠C=∠BEC∠BEF+∠FEC=∠BEC(已知)
∴∠B+∠C=∠BEF+∠FEC(等量代換)
∴∠ =∠ (等式性質)
∴EF∥
∵EF∥AB
∴AB∥CD(平行于同一條直線的兩條直線互相平行)
(2)請再選用一種方法,加以證明
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AD是BC邊上的高,AE、BF分別是∠BAC、∠ABC的平分線,∠BAC=50°,∠ABC=60°,則∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC中,E、F分別為線段AB、AC上的點(不與A、B、C重合).
(1)如圖1,若EF∥BC,求證:![]()
(2)如圖2,若EF不與BC平行,(1)中的結論是否仍然成立?請說明理由;
(3)如圖3,若EF上一點G恰為△ABC的重心,![]() ,求
,求![]() 的值.
的值.
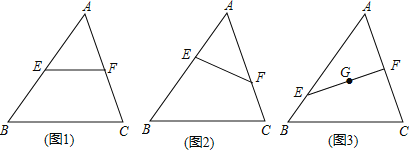
查看答案和解析>>
科目:初中數學 來源: 題型:
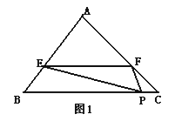
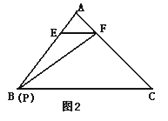
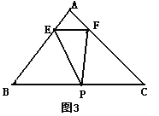
【題目】如圖1,某人用一張面積為S的三角形紙片ABC剪出一個△EFP,記△EFP的面積為T,已知E、F、P分別是△ABC三邊上的三點,且EF∥BC.
(1)如圖2,當P與B重合,設![]() 分別等于
分別等于![]() 、
、![]() 、
、![]() 時,△PEF的面積分別為
時,△PEF的面積分別為![]() 、
、![]() 、
、![]() .
.
① ![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
② 寫出![]() 的求解過程;
的求解過程;
(2)如圖3,當點P是△ABC邊BC上的任意一點時(點P可與B或C重合),設![]() , 試求出
, 試求出![]() 與
與![]() 、S的函數關系式;
、S的函數關系式;
(3)請探究T是否存在最大值,若存在,請求出這個最大值;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com