
【題目】如圖,在平面直角坐標系xOy中,點C的坐標為(4,0),一次函數 ![]() 的圖像分別交x軸、y軸于點A、點B.
的圖像分別交x軸、y軸于點A、點B.
(1)若點D是直線AB在第一象限內的點,且BD=BC,試求出點D的坐標.
(2)在⑴的條件下,若點Q是坐標軸上的一個動點,試探索在第一象限是否存在另一個點P,使得以B、D、P、Q為頂點的四邊形是菱形(BD為菱形的一邊)?若存在,請直接寫出點P的坐標;若不存在,請說明理由.
【答案】
(1)解:如圖1,設點D(3a,4a+3),
過點D作DE⊥y軸于E,把x=0代入y= ![]() x+3中,得,y=3,
x+3中,得,y=3,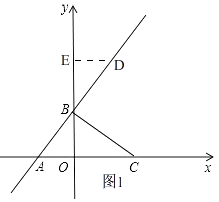
∴OB=3,
∴BE=OE-OB=4a+3-3=4a,BC= ![]() =5,
=5,
在Rt△BED中,根據勾股定理得,(3a)2+(4a)2=52 ,
∴a=±1,
∵點D在第一象限,
∴a=1,
∴D(3,7)
(2)解:由(1)知,BD=BC=5,
①當點Q在y軸上時,
設Q(0,q),
∵使得以B,D,P,Q為頂點的四邊形是菱形(BD為菱形的一邊),且點P在第一象限內,
即:四邊形BDPQ是菱形,
∴PQ∥BD,DP∥BQ,
∴點P的橫坐標為3,
∵四邊形BDPQ是菱形,
∴BQ=BD=5,
∵B(0,3),
∴Q(0,8)或(0,-2),
Ⅰ、當點Q(0,8)時,
∵直線BD的解析式為y= ![]() x+3,
x+3,
∴直線PQ的解析式為y= ![]() x+8,
x+8,
當x=3時,y=12,
∴P(3,12),
Ⅱ、點Q(0,-2)時,
∵直線BD的解析式為y= ![]() x+3,
x+3,
∴直線PQ的解析式為y= ![]() x-2,
x-2,
當x=3時,y=2,
∴P(3,2),
②當點Q在x軸上時,
設Q(m,0),),
∵使得以B,D,P,Q為頂點的四邊形是菱形(BD為菱形的一邊),且點P在第一象限內,
即:四邊形BDPQ是菱形,
∴BQ=BD=5,
∵OB=3,
∴OQ=4,
∴Q(-4,0)或(4,0)
Ⅰ、當Q(-4,0)時,∵一次函數y= ![]() x+3的圖象交x軸于點A,
x+3的圖象交x軸于點A,
∴A(- ![]() ,0),
,0),
∴點Q在點A的左側,
∴點P在第二象限內,不符合題意,舍去,
Ⅱ、當點Q(4,0)時,∵四邊形BDPQ是菱形,
∴BQ∥DP,PQ∥BD,
∵直線BD的解析式為y= ![]() x+3,
x+3,
∴設直線PQ的解析式為y= ![]() x+b,
x+b,
∴ ![]() ×4+b=0,
×4+b=0,
∴b=- ![]() ,
,
∴直線PQ的解析式為y= ![]() x-
x- ![]() ①,
①,
∵B(0,3),Q(4,0),
∴直線BQ的解析式為y=- ![]() x+3,
x+3,
∵D(3,7),
∴直線DP的解析式為y=- ![]() x+
x+ ![]() ②,
②,
聯立①②解得,x=7,y=4,
∴P(7,4),
即:滿足條件的點P的坐標為(3,12)、(3,2)、(7,4).
【解析】(1)過點D作DE⊥y軸于E,先求出直線AB與y軸的交點坐標,再根據勾股定理求出BC的長,然后在Rt△BED中用勾股定理建立方程求出a的值,就可求得點D的坐標。
(2)分兩種情況討論:①當點Q在y軸上時,利用菱形的性質求出BQ=5,再求出點Q的坐標為(0,8)或(0,-2),然后利用菱形的性質求出當點Q為(0,8)和(0,-2)時的點P的坐標;②當點Q在x軸上時,先求出點Q的坐標為(-4,0)或(4,0),然后利用菱形的性質分別求出點Q的坐標為(-4,0)和(4,0)時的點P的坐標。


 浙大優學小學年級銜接導與練浙江大學出版社系列答案
浙大優學小學年級銜接導與練浙江大學出版社系列答案 小學暑假作業東南大學出版社系列答案
小學暑假作業東南大學出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業江西人民出版社系列答案
波波熊暑假作業江西人民出版社系列答案科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,∠C=90°,AC=BC,點D是AB的中點,分別過點D作DE⊥AC,DF⊥BC,垂足分別為點E、F.求證:四邊形CEDF是正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下表是一組二次函數y=x2+3x﹣5的自變量x與函數值y的對應值:
x | 1 | 1.1 | 1.2 | 1.3 | 1.4 |
y | ﹣1 | ﹣0.49 | 0.04 | 0.59 | 1.16 |
那么方程x2+3x﹣5=0的一個近似根是( )
A.1
B.1.1
C.1.2
D.1.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖①,在一條筆直的公路上有M、P、N三個地點,M、P兩地相距20km,甲開汽車,乙騎自行車分別從M、P兩地同時出發,勻速前往N地,到達N地后停止運動.已知乙騎自行車的速度為20km/h,甲,乙兩人之間的距離y(km)與乙行駛的時間t(h)之間的關系如圖②所示.
(1)M、N兩地之間的距離為 km;
(2)求線段BC所表示的y與t之間的函數表達式;
(3)若乙到達N地后,甲,乙立即以各自原速度返回M地,請在圖②所給的直角坐標系中補全函數圖象.

查看答案和解析>>
科目:初中數學 來源: 題型:
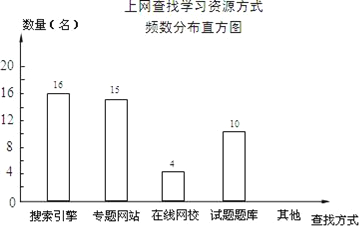
【題目】某學校為了了解本校學生采用何種方式上網查找所需要的學習資源,隨機抽取部分學生了解情況,并將統計結果繪制成頻數分布表及頻數分布直方圖.
上網查找學習資源方式頻數分布表
查找方式 | 頻數 | 頻率 |
搜索引擎 | 16 | 32% |
專題網站 | 15 | a |
在線網校 | 4 | 8% |
試題題庫 | 10 | 20% |
其他 | b | 10% |
(1)頻數分布表中a,b的值:a= ;b= ;
(2)補全頻數分布直方圖;
(3)若全校有1000名學生,估計該校利用搜索引擎上網查找學習資源的學生有多少名?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:用2輛A型車和1輛B型車裝滿貨物一次可運貨10噸;用1輛A型車和2輛B型車裝滿貨物一次可運貨11噸.某物流公司現有31噸貨物,計劃同時租用A型車![]() 輛,B型車
輛,B型車![]() 輛,一次運完,且恰好每輛車都裝滿貨物. 根據以上信息,解答下列問題:
輛,一次運完,且恰好每輛車都裝滿貨物. 根據以上信息,解答下列問題:
(1)1輛A型車和1輛B型車都裝滿貨物一次可分別運貨多少噸?
(2)請你幫該物流公司設計租車方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com