

| 解:(1)△APQ∽△BCP; (2)當P為AB中點時,有AQ+BC=CQ, 證明:連接CQ,延長QP交CB的延長線于點E, 可證△APQ≌△BPE, 則AQ=BE,PQ= PE, 又因為CP⊥QE,可得CQ= CE, 所以AQ+BC=CQ; (3)當AQ=  時,有PC=3PQ, 時,有PC=3PQ,證明:在正方形ABCD中,∠A=∠B=90°,AD=BC=AB, 又因為直角三角板的頂點P在邊AB上, 所以∠1+∠2=180°-∠QPC=90°, 因為Rt△CBP中,∠3+∠2=90°, 所以∠1=∠3, 所以△APQ∽△BCP, 所以  因為AQ=  , ,所以  所以AP=  ,或AP= ,或AP= (不合題意,舍去), (不合題意,舍去),所以  , ,所以PC=3PQ。 |
  |


科目:初中數學 來源: 題型:
 的另一條直角邊與AD交于點Q.
的另一條直角邊與AD交于點Q.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 的另一條直角邊與AD交于點Q.
的另一條直角邊與AD交于點Q.查看答案和解析>>
科目:初中數學 來源: 題型:
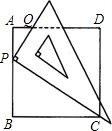
已知:如圖,一塊三角板的直角頂點P放在正方形ABCD的AB邊上,并且使一條直角邊經過點C,三角板的另一條直角邊與AD交于點Q.

(1)請你寫出此時圖形中成立的一個結論(任選一個);
(2)當點P滿足什么條件時,有AQ+BC=CQ,請證明你的結論;
(3)當點Q在AD的什么位置時,可證得PC=3PQ,并寫出論證的過程.
查看答案和解析>>
科目:初中數學 來源:2008年北京市海淀區中考數學一模試卷(解析版) 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com