
條件:如下左圖,![]() 、
、![]() 是直線
是直線![]() 同旁的兩個定點.問題:在直線
同旁的兩個定點.問題:在直線![]() 上確定一點
上確定一點![]() ,使
,使![]() 的值最小.方法:作點
的值最小.方法:作點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,連結
,連結![]() 交
交![]() 于點
于點![]() ,則
,則![]() 的值最小(不必證明).
的值最小(不必證明).
模型應用:
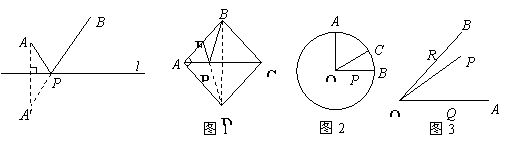
(1)如圖1,正方形![]() 的邊長為2,
的邊長為2,![]() 為
為![]() 的中點,
的中點,![]() 是
是![]() 上一動點.連結
上一動點.連結![]() ,由正方形對稱性可知,
,由正方形對稱性可知,![]() 與
與![]() 關于直線
關于直線![]() 對稱.連結
對稱.連結![]() 交
交![]() 于
于![]() ,則
,則![]() 的最小值是___________;
的最小值是___________;
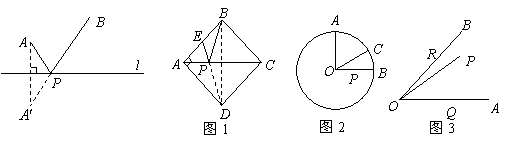
(2)如圖2,![]() 的半徑為2,點
的半徑為2,點![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 是
是![]() 上一動點,求
上一動點,求![]() 的最小值;
的最小值;
(3)如圖3,![]() ,
,![]() 是
是![]() 內一點,
內一點,![]() ,
,![]() 分別是
分別是![]() 上的動點,求
上的動點,求![]() 周長的最小值.
周長的最小值.
 口算題卡加應用題集訓系列答案
口算題卡加應用題集訓系列答案 綜合自測系列答案
綜合自測系列答案科目:初中數學 來源: 題型:
幾何模型:
條件:如下左圖,![]() 、
、![]() 是直線
是直線![]() 同旁的兩個定點.
同旁的兩個定點.
問題:在直線![]() 上確定一點
上確定一點![]() ,使
,使![]() 的值最小.
的值最小.
方法:作點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,連結
,連結![]() 交
交![]() 于點
于點![]() ,則
,則![]() 的值最小(不必證明).
的值最小(不必證明).
模型應用:
(1)如圖1,正方形![]() 的邊長為2,
的邊長為2,![]() 為
為![]() 的中點,
的中點,![]() 是
是![]() 上一動點.連結
上一動點.連結![]() ,由正方形對稱性可知,
,由正方形對稱性可知,![]() 與
與![]() 關于直線
關于直線![]() 對稱.連結
對稱.連結![]() 交
交![]() 于
于![]() ,則
,則![]() 的最小值是___________;
的最小值是___________;
(2)如圖2,![]() 的半徑為2,點
的半徑為2,點![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 是
是![]() 上一動點,求
上一動點,求![]() 的最小值;
的最小值;
(3)如圖3,![]() ,
,![]() 是
是![]() 內一點,
內一點,![]() ,
,![]() 分別是
分別是![]() 上的動點,求
上的動點,求![]() 周長的最小值.
周長的最小值.
查看答案和解析>>
科目:初中數學 來源:模擬題 題型:探究題
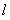 同旁的兩個定點.
同旁的兩個定點. 上確定一點P,使
上確定一點P,使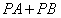 的值最小.
的值最小.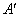 ,連結
,連結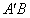 交l點P,則
交l點P,則 的值最小(不必證明)。
的值最小(不必證明)。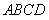 的邊長為2,E為的AB中點,P是AC上一動點.連結
的邊長為2,E為的AB中點,P是AC上一動點.連結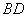 ,由正方形對稱性可知,B與D關于直線
,由正方形對稱性可知,B與D關于直線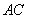 對稱.連結
對稱.連結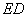 交AC于P,則
交AC于P,則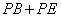 的最小值是_____ ;
的最小值是_____ ;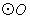 的半徑為2,點
的半徑為2,點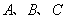 在
在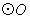 上,
上,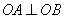 ,
,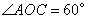 ,P是OB上一動點,求
,P是OB上一動點,求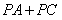 的最小值;
的最小值;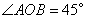 ,P是
,P是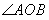 內一點,
內一點,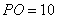 ,
,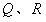 分別是
分別是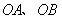 上的動點,求
上的動點,求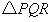 周長的最小值。
周長的最小值。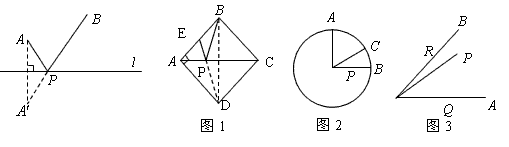
查看答案和解析>>
科目:初中數學 來源: 題型:
幾何模型:
條件:如下左圖,![]() 、
、![]() 是直線
是直線![]() 同旁的兩個定點.
同旁的兩個定點.
問題:在直線![]() 上確定一點
上確定一點![]() ,使
,使![]() 的值最小.
的值最小.
方法:作點![]() 關于直線
關于直線![]() 的對稱點
的對稱點![]() ,連結
,連結![]() 交
交![]() 于點
于點![]() ,則
,則![]() 的值最小(不必證明).
的值最小(不必證明).
模型應用:
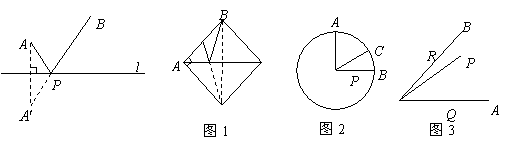
(1)如圖1,正方形![]() 的邊長為2,
的邊長為2,![]() 為
為![]() 的中點,
的中點,![]() 是
是![]() 上一動點.連結
上一動點.連結![]() ,由正方形對稱性可知,
,由正方形對稱性可知,![]() 與
與![]() 關于直線
關于直線![]() 對稱.連結
對稱.連結![]() 交
交![]() 于
于![]() ,則
,則![]() 的最小值是___________;
的最小值是___________;
(2)如圖2,![]() 的半徑為2,點
的半徑為2,點![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,![]() 是
是![]() 上一動點,求
上一動點,求![]() 的最小值;
的最小值;
(3)如圖3,![]() ,
,![]() 是
是![]() 內一點,
內一點,![]() ,
,![]() 分別是
分別是![]() 上的動點,求
上的動點,求![]() 周長的最小值.
周長的最小值.
 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com