
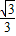 ,那么另一組數據2x1-1,2x2-1,2x3-1,2x4-1,2x5-1的平均數與標準差分別是( )
,那么另一組數據2x1-1,2x2-1,2x3-1,2x4-1,2x5-1的平均數與標準差分別是( )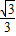


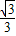
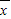 =
= (x1+x2+…+x5)=2,
(x1+x2+…+x5)=2, [(x1-2)2+(x2-2)2+…+(x5-2)2]=(
[(x1-2)2+(x2-2)2+…+(x5-2)2]=( )2=
)2= ,
, 2=
2= [2x1-1+2x2-1+…+x5-1]=
[2x1-1+2x2-1+…+x5-1]= [2(x1+x2+…+xn)-5]
[2(x1+x2+…+xn)-5] ×2(x1+x2+…+x5)-1
×2(x1+x2+…+x5)-1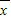 -1=4-1=3,
-1=4-1=3, [(2x1-1-3)2+(2x2-1-3)2+…+(2x5-1-3)2]=
[(2x1-1-3)2+(2x2-1-3)2+…+(2x5-1-3)2]= {4[(x1-2)2+(x2-2)2+…+(x5-2)2]}=4S2=
{4[(x1-2)2+(x2-2)2+…+(x5-2)2]}=4S2= ,
,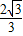 .
.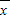 ;②計算偏差,即每個數據與平均數的差;③計算偏差的平方和;④偏差的平方和除以數據個數.標準差即方差的算術平方根;注意標準差和方差一樣都是非負數.
;②計算偏差,即每個數據與平均數的差;③計算偏差的平方和;④偏差的平方和除以數據個數.標準差即方差的算術平方根;注意標準差和方差一樣都是非負數. 

 名題金卷系列答案
名題金卷系列答案科目:初中數學 來源: 題型:
 下列說法正確的是
下列說法正確的是| 2m |
| x-2 |
| 3x |
| 2-x |
| 1 |
| x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com