
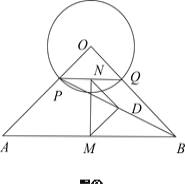
【題目】如圖本題圖①,在等腰Rt![]() 中,
中,![]() ,
,![]() ,
,![]() 為線段
為線段![]() 上一點,以
上一點,以![]() 為半徑作
為半徑作![]() 交
交![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,線段
,線段![]() 、
、![]() 、
、![]() 的中點分別為
的中點分別為![]() 、
、![]() 、
、![]() .
.
(1)試探究![]() 是什么特殊三角形?說明理由;
是什么特殊三角形?說明理由;
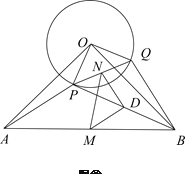
(2)將![]() 繞點
繞點![]() 逆時針方向旋轉到圖②的位置,上述結論是否成立?并證明結論;
逆時針方向旋轉到圖②的位置,上述結論是否成立?并證明結論;
(3)若![]() ,把
,把![]() 繞點
繞點![]() 在平面內自由旋轉,求
在平面內自由旋轉,求![]() 的面積y的最大值與最小值的差.
的面積y的最大值與最小值的差.
【答案】(1)![]() 為等腰直角三角形;(2)
為等腰直角三角形;(2)![]() 仍然為等腰直角三角形;(3)
仍然為等腰直角三角形;(3)![]() 的最大值與最小值的差為:
的最大值與最小值的差為:![]()
【解析】分析:(1)由OA=OB,OP=OQ可得AP=BQ,再利用三角形的中位線可得△DMN是等腰直角三角形;
(2)由旋轉的性質得∠AOP=∠BOQ,從而可證△AOP≌△BOQ,由三角形中位線的性質可得DM=DN,根據平行線的性質和三角形內角和可證∠MDN=90°,從而結論得證;
(3)如圖,設⊙![]() 交
交![]() 于點
于點![]() ,交
,交![]() 延長線于點
延長線于點![]() ,連接
,連接![]() ,
,![]() ,
,![]() .由三角形三邊的關系得
.由三角形三邊的關系得![]() ,
,![]() ,由三角形的面積公式得
,由三角形的面積公式得![]() ,從而可求出y的最大值和最小值,然后相減即可.
,從而可求出y的最大值和最小值,然后相減即可.
詳解:(1)![]() 為等腰直角三角形
為等腰直角三角形
![]()
![]() 分別為
分別為![]() 的中點,
的中點,
![]()
![]() 且
且![]()
同理:![]()
![]()
![]()
![]()
![]() .
.
又![]()
![]()
![]()
![]() 即
即![]() 為等腰直角三角形.
為等腰直角三角形.
(2)如圖,![]() 仍然為等腰直角三角形.
仍然為等腰直角三角形.
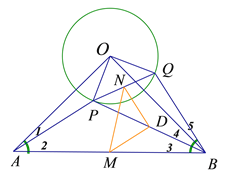
證明:由旋轉的性質,![]() .
.
![]()
![]()
![]()
![]() ≌
≌![]() ,
,
![]()
![]() .
.
![]()
![]() 分別為
分別為![]() 的中點,
的中點,![]()
![]() 且
且![]()
同理:![]() ,
,![]()
![]()
在等腰Rt![]() 中,
中,![]()
![]()
![]()
![]()
![]()
![]()
![]() 同理:
同理:![]()
![]()
![]()
=![]()
![]() .
.
![]()
![]()
![]()
![]() 為等腰直角三角形.
為等腰直角三角形.
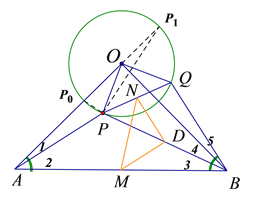
(3), 如圖,設⊙![]() 交
交![]() 于點
于點![]() ,交
,交![]() 延長線于點
延長線于點![]() ,
,
連接![]()
![]() ,而
,而![]() ,
,
![]() 同理,
同理,![]()
由題意,![]() ,
,
![]()
![]() 的最小值為
的最小值為![]() . 同理,
. 同理,![]() 最大值為
最大值為![]() ,
,
從而得![]() 的最大值與最小值的差為:
的最大值與最小值的差為:![]()


 優學名師名題系列答案
優學名師名題系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠C=90°,∠BAC的平分線交BC于點D,點O在AB上,以點O為圓心,OA為半徑的圓恰好經過點D,分別交AC,AB于點E,F.
(1)試判斷直線BC與⊙O的位置關系,并說明理由;
(2)若BD=2![]() ,BF=2,求陰影部分的面積(結果保留π).
,BF=2,求陰影部分的面積(結果保留π).

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校組織學生書法比賽,對參賽作品按A、B、C、D四個等級進行了評定.現隨機取部分學生書法作品的評定結果進行分析,并繪制扇形統計圖和條形統計圖如下:

根據上述信息完成下列問題:
(1)求這次抽取的樣本的容量;
(2)請在圖②中把條形統計圖補充完整;
(3)已知該校這次活動共收到參賽作品750份,請你估計參賽作品達到B級以上(即A級和B級)有多少份?
查看答案和解析>>
科目:初中數學 來源: 題型:
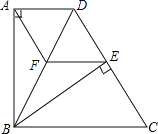
【題目】如圖,四邊形ABCD中,AD∥BC,BA⊥AD,BC=DC,BE⊥CD于點E.
(1)求證:△ABD≌△EBD;
(2)過點E作EF∥DA,交BD于點F,連接AF.求證:四邊形AFED是菱形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某文化用品商店用1 000元購進一批“晨光”套尺,很快銷售一空;商店又用1 500元購進第二批該款套尺,購進時單價是第一批的![]() 倍,所購數量比第一批多100套.
倍,所購數量比第一批多100套.
(1)求第一批套尺購進時單價是多少?
(2)若商店以每套4元的價格將這兩批套尺全部售出,可以盈利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:二次函數![]() ,當
,當![]() 時,函數有最大值5.
時,函數有最大值5.
(1)求此二次函數圖象與坐標軸的交點;
(2)將函數![]() 圖象x軸下方部分沿x軸向上翻折,得到的新圖象與直線
圖象x軸下方部分沿x軸向上翻折,得到的新圖象與直線![]() 恒有四個交點,從左到右,四個交點依次記為
恒有四個交點,從左到右,四個交點依次記為![]() ,當以
,當以![]() 為直徑的圓與
為直徑的圓與![]() 軸相切時,求
軸相切時,求![]() 的值.
的值.
(3)若點![]() 是(2)中翻折得到的拋物線弧部分上任意一點,若關于m的一元二次方程
是(2)中翻折得到的拋物線弧部分上任意一點,若關于m的一元二次方程![]() 恒有實數根時,求實數k的最大值.
恒有實數根時,求實數k的最大值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩人利用不同的交通工具,沿同一路線分別從A、B兩地同時出發勻速前往C地(B在A、C兩地的途中).設甲、乙兩車距A地的路程分別為y甲、y乙(千米),行駛的時間為x(小時),y甲、y乙與x之間的函數圖象如圖所示.
(1)直接寫出y甲、y乙與x之間的函數表達式;
(2)如圖,過點(1,0)作x軸的垂線,分別交y甲、y乙的圖象于點M,N.求線段MN的長,并解釋線段MN的實際意義;
(3)在乙行駛的過程中,當甲、乙兩人距A地的路程差小于30千米時,求x的取值范圍.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用火柴棒按下列方式搭建三角形:
![]()
三角形個數 | 1 | 2 | 3 | 4 | … |
火柴棒根數 | 3 | 5 | 7 | 9 | … |
(1)當三角形的個數為n時,火柴棒的根數是多少?
(2)求當n=100時,有多少根火柴棒?
(3)當火柴棒的根數為2017時,三角形的個數是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】七(1)班的學習小組學習“線段中點”內容時,得到一個很有意思的結論,請跟隨他們一起思考.
(1)發現:
如圖1,線段![]() ,點
,點![]() 在線段
在線段![]() 上,當點
上,當點![]() 是線段
是線段![]() 和線段
和線段![]() 的中點時,線段
的中點時,線段![]() 的長為_________;若點
的長為_________;若點![]() 在線段
在線段![]() 的延長線上,其他條件不變(請在圖2中按題目要求將圖補充完整),得到的線段
的延長線上,其他條件不變(請在圖2中按題目要求將圖補充完整),得到的線段![]() 與線段
與線段![]() 之間的數量關系為_________.
之間的數量關系為_________.

(2)應用:
如圖3,現有長為40米的拔河比賽專用繩![]() ,其左右兩端各有一段(
,其左右兩端各有一段(![]() 和
和![]() )磨損了,磨損后的麻繩不再符合比賽要求. 已知磨損的麻繩總長度不足20米. 小明認為只利用麻繩
)磨損了,磨損后的麻繩不再符合比賽要求. 已知磨損的麻繩總長度不足20米. 小明認為只利用麻繩![]() 和一把剪刀(剪刀只用于剪斷麻繩)就可以得到一條長20米的拔河比賽專用繩
和一把剪刀(剪刀只用于剪斷麻繩)就可以得到一條長20米的拔河比賽專用繩![]() . 小明所在學習小組認為此法可行,于是他們應用“線段中點”的結論很快做出了符合要求的專用繩
. 小明所在學習小組認為此法可行,于是他們應用“線段中點”的結論很快做出了符合要求的專用繩![]() ,請你嘗試著“復原”他們的做法:
,請你嘗試著“復原”他們的做法:
①在圖中標出點![]() 、點
、點![]() 的位置,并簡述畫圖方法;
的位置,并簡述畫圖方法;
②請說明①題中所標示![]() 點的理由.
點的理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com