
在正方形ABCD中,過點A引射線AH,交邊CD于點H(點H與點D不重合).通過翻折,使點B落在射線AH上的點G處,折痕AE交BC于E,延長EG交CD于F.
【感知】如圖1,當點H與點C重合時,可得FG=FD.
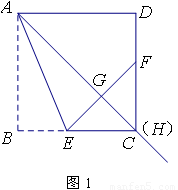
【探究】如圖2,當點H為邊CD上任意一點時,猜想FG與FD的數量關系,并說明理由.

【應用】在圖2中,當AB=5,BE=3時,利用探究結論,求FG的長.
【探究】FG=FD;【應用】 .
.
【解析】
試題分析:【探究】連接AF,根據圖形猜想FD=FG,由折疊的性質可得AB=AG=AD,再結合AF為△AGF和△ADF的公共邊,從而證明△AGF≌△ADF,從而得出結論.
【應用】設FG=x,則FC=5-x,FE=3+x,在RT△ECF中利用勾股定理可求出x的值,進而可得出答案.
【探究】猜想FD=FG.
連接AF,

由折疊的性質可得AB=AG=AD,
在Rt△AGF和Rt△ADF中,
 ,
,
∴△AGF≌△ADF.
∴FG=FD;
【應用】設GF= ,則CF=5-
,則CF=5- ,則EF=
,則EF= +3
+3
在△ECF中由勾股定理得, ,解得
,解得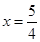
∴FG的長為 .
.
考點:翻折變換及正方形的性質
點評:,掌握△AGF≌△ADF始終不變是解答本題的關鍵,另外在進行結論的應用時,得出Rt△EFC的各邊后運用勾股定理進行求解時,要細心避免出錯.


 浙江名校名師金卷系列答案
浙江名校名師金卷系列答案科目:初中數學 來源: 題型:
 18、在正方形ABCD中,點G是BC上任意一點,連接AG,過B,D兩點分別作BE⊥AG,DF⊥AG,垂足分別為E,F兩點,求證:△ADF≌△BAE.
18、在正方形ABCD中,點G是BC上任意一點,連接AG,過B,D兩點分別作BE⊥AG,DF⊥AG,垂足分別為E,F兩點,求證:△ADF≌△BAE.查看答案和解析>>
科目:初中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 2 |

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com