
【題目】如圖,在![]() 中,
中,![]() ,延長
,延長![]() 使
使![]() ,線段
,線段![]() 繞點C順時針旋轉90°得到線段
繞點C順時針旋轉90°得到線段![]() ,連結
,連結![]() .
.
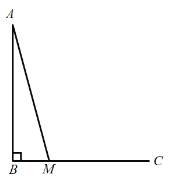
(1)依據題意補全圖形;
(2)當![]() 時,
時,![]() 的度數是__________;
的度數是__________;
(3)小聰通過畫圖、測量發現,當![]() 是一定度數時,
是一定度數時,![]() .
.
小聰把這個猜想和同學們進行交流,通過討論,形成了證明該猜想的幾種想法:
想法1:通過觀察圖形可以發現,如果把梯形![]() 補全成為正方形
補全成為正方形![]() ,就易證
,就易證![]() ,因此易得當
,因此易得當![]() 是特殊值時,問題得證;
是特殊值時,問題得證;
想法2:要證![]() ,通過第(2)問,可知只需要證明
,通過第(2)問,可知只需要證明![]() 是等邊三角形,通過構造平行四邊形
是等邊三角形,通過構造平行四邊形![]() ,易證
,易證![]() ,通過
,通過![]() ,易證
,易證![]() ,從而解決問題;
,從而解決問題;
想法3:通過![]() ,連結
,連結![]() ,易證
,易證![]() ,易得
,易得![]() 是等腰三角形,因此當
是等腰三角形,因此當![]() 是特殊值時,問題得證.
是特殊值時,問題得證.
請你參考上面的想法,幫助小聰證明當![]() 是一定度數時,
是一定度數時,![]() .(一種方法即可)
.(一種方法即可)
 優生樂園系列答案
優生樂園系列答案 新編小學單元自測題系列答案
新編小學單元自測題系列答案科目:初中數學 來源: 題型:
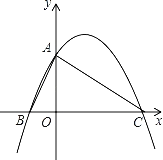
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象與y軸交于點A(0,4),與x軸負半軸交于B,與正半軸交于點C(8,0),且∠BAC=90°.
(1)求該二次函數解析式;
(2)若N是線段BC上一動點,作NE∥AC,交AB于點E,連結AN,當△ANE面積最大時,求點N的坐標;
(3)若點P為x軸上方的拋物線上的一個動點,連接PA、PC,設所得△PAC的面積為S.問:是否存在一個S的值,使得相應的點P有且只有2個?若有,求出這個S的值,并求此時點P的橫坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
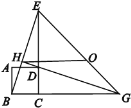
【題目】如圖,四邊形ABCD是正方形,ΔECG是等腰直角三角形,∠BGE的平分線過點D交BE 于H,O是EG的中點,對于下面四個結論:①GH⊥BE;②OH∥BG,且![]() ;③
;③![]() ;④△EBG的外接圓圓心和它的內切圓圓心都在直線HG上.其中表述正確的個數是( )
;④△EBG的外接圓圓心和它的內切圓圓心都在直線HG上.其中表述正確的個數是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】探索應用
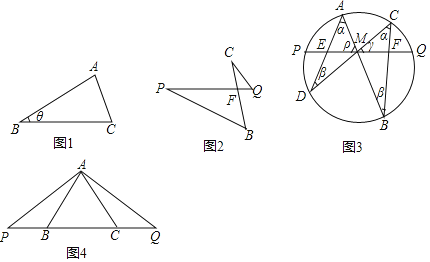
材料一:如圖1,在△ABC中,AB=c,BC=a,∠B=θ,用c和θ表示BC邊上的高為 ,用a.c和θ表示△ABC的面積為 .
材料二:如圖2,已知∠C=∠P,求證:CFBF=QFPF.
材料三:蝴蝶定理(ButterflyTheorem)是古代歐氏平面幾何中最精彩的結果之一,最早出現在1815年,由W.G.霍納提出證明,定理的圖形象一只蝴蝶.
定理:如圖3,M為弦PQ的中點,過M作弦AB和CD,連結AD和BC交PQ分別于點E和F,則ME=MF.
證明:設∠A=∠C=α,∠B=∠D=β,
∠DMP=∠CMQ=γ,∠AMP=∠BMQ=ρ,
PM=MQ=a,ME=x,MF=y
由![]()
即![]()
化簡得:MF2AEED=ME2CFFB
則有:![]() ,
,
又∵CFFB=QFFP,AEED=PEEQ,
∴![]() ,即
,即![]()
即![]() ,從而x=y,ME=MF.
,從而x=y,ME=MF.
請運用蝴蝶定理的證明方法解決下面的問題:
如圖4,B、C為線段PQ上的兩點,且BP=CQ,A為PQ外一動點,且滿足∠BAP=∠CAQ,判斷△PAQ的形狀,并證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是某企業甲、乙兩位員工的能力測試結果的網狀圖,以O為圓心的五個同心圓分別代表能力水平的五個等級由低到高分別賦分1至5分,由原點出發的五條線段分別指向能力水平的五個維度,網狀圖能夠更加直觀的描述測試者的優勢和不足,觀察圖形,有以下幾個推斷:
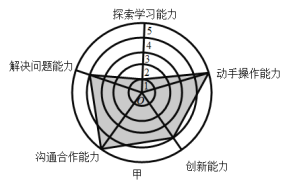
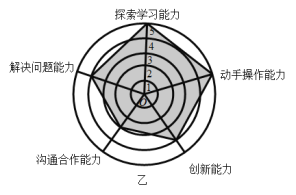
①甲和乙的動手操作能力都很強;
②缺少探索學習的能力是甲自身的不足;
③與甲相比乙需要加強與他人的溝通合作能力;
④乙的綜合評分比甲要高.
其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下面是小王同學“過直線外一點作該直線的平行線”的尺規作圖過程.
已知:直線l及直線l外一點P.
求作:直線![]() ,使得
,使得![]() .
.

作法:如圖,
①在直線l外取一點A,作射線![]() 與直線l交于點B,
與直線l交于點B,
②以A為圓心,![]() 為半徑畫弧與直線l交于點C,連接
為半徑畫弧與直線l交于點C,連接![]() ,
,
③以A為圓心,![]() 為半徑畫弧與線段
為半徑畫弧與線段![]() 交于點
交于點![]() ,
,
則直線![]() 即為所求.
即為所求.
根據小王設計的尺規作圖過程,,
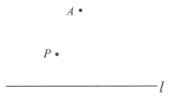
(1)使用直尺和圓規,補全圖形;(保留作圖痕跡)
(2)完成下面的證明.
證明:∵![]() ,
,
∴![]() ,(______________________)(填推理的依據).
,(______________________)(填推理的依據).
∵![]() __________,
__________,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() (____________________)(填推理的依據).
(____________________)(填推理的依據).
即![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點A,B,C,D在⊙O上,弦AD的延長線與弦BC的延長線相交于點E.用①AB是⊙O的直徑,②CB=CE,③AB=AE中的兩個作為題設,余下的一個作為結論組成一個命題,則組成真命題的個數為( )
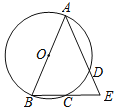
A.0B.1C.2D.3
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,△ABC中,AB=AC,以AB為直徑的⊙O與BC相交于點D,與CA的延長線相交于點E,過點D作DF⊥AC于點F.

(1)試說明DF是⊙O的切線;
(2)若AC=3AE,求tanC.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綜合與探究
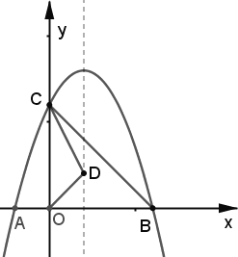
如圖,拋物線![]() 與
與![]() 軸交于
軸交于![]() 兩點(點
兩點(點![]() 在點
在點![]() 的左側),與
的左側),與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,點
,點![]() 為拋物線對稱軸上一動點.
為拋物線對稱軸上一動點.
(1)求直線![]() 的函數表達式;
的函數表達式;
(2)連接![]() ,求
,求![]() 周長的最小值;
周長的最小值;
(3)在拋物線上是否存在一點![]() .使以
.使以![]() 為頂點的四邊形是以
為頂點的四邊形是以![]() 為邊的平行四邊形?若存在,請直接寫出
為邊的平行四邊形?若存在,請直接寫出![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com