
【題目】如圖,在反比例函數y= ![]() 的圖象上有一動點A,連接AO并延長交圖象的另一支于點B,在第二象限內有一點C,滿足AC=BC,當點A運動時,點C始終在函數y=
的圖象上有一動點A,連接AO并延長交圖象的另一支于點B,在第二象限內有一點C,滿足AC=BC,當點A運動時,點C始終在函數y= ![]() 的圖象上運動,若tan∠CAB=2,則k的值為( )
的圖象上運動,若tan∠CAB=2,則k的值為( )
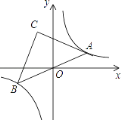
A. ﹣3 B. ﹣6 C. ﹣9 D. ﹣12
【答案】B
【解析】
連接OC,過點A作AE⊥x軸于點E,過點C作CF⊥y軸于點F,通過同角的余角相等得出∠AOE=∠COF,結合“∠AEO=90°,∠CFO=90°”可得出△AOE∽△COF,根據相似三角形的性質得出比例式,再由tan∠CAB=2,可得出CFOF的值,進而得到k的值.
解:如圖,連接OC,過點A作AE⊥y軸于點E,過點C作CF⊥y軸于點F,
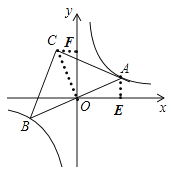
∵直線AB過點O,點A、B在反比例函數y=![]() 的圖像上,
的圖像上,
∴點A、B點關于O點對稱,
∴AO=BO.
又∵AC=BC,
∴CO⊥AB.
∵∠AOE+∠AOF=90°,∠AOF+∠COF=90°,
∴∠AOE=∠COF,
又∵∠AEO=90°,∠CFO=90°,
∴△AOE∽△COF,
∴![]() =
=![]() =
=![]() ,
,
∵tan∠CAB=![]() =2,
=2,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴CF=2AE,OF=2OE.
又∵AEOE=![]() ,
,
∴CFOF=|k|=4 AEOE=6,
∴k=±6.
∵點C在第二象限,
∴k=-6,
故選:B.


科目:初中數學 來源: 題型:
【題目】今年3月5日,我校組織全體學生參加了“走出校門,服務社會”的活動.九年級三班同學統計了該天本班學生打掃街道,去敬老院服務和到社區文藝演出的人數,并做了如下直方圖和扇形統計圖.請根據同學所作的兩個圖形.解答:
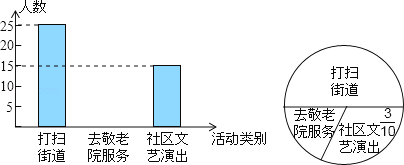
(1)九年級三班有多少名學生;
(2)補全直方圖的空缺部分;
(3)若九年級有800名學生,估計該年級去敬老院的人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線,![]() 與
與![]() 軸交于
軸交于![]() 兩點,與
兩點,與![]() 軸交于點
軸交于點![]() ,且拋物線
,且拋物線![]() 的對稱軸為直線
的對稱軸為直線![]() .
.
(1)拋物線的表達式;
(2)若拋物線![]() 與拋物線
與拋物線![]() 關于直線
關于直線![]() 對稱,拋物線
對稱,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() 兩點(點
兩點(點![]() 在點
在點![]() 左側),要使
左側),要使![]() ,求所有滿足條件的拋物線
,求所有滿足條件的拋物線![]() 的表達式.
的表達式.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知菱形ABCD的邊長為2cm,∠A=60°,點M從點A出發,以1cm/s的速度向點B運動,點N從點A同時出發,以2cm/s的速度經過點D向點C運動,當其中一個動點到達端點時,另一個動點也隨之停止運動.則△AMN的面積y(cm2)與點M運動的時間t(s)的函數的圖象大致是( )
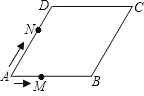
A. 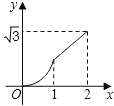 B.
B. 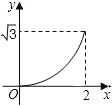
C. 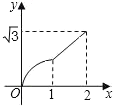 D.
D. 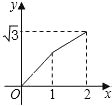
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某書店為了迎接“讀書節”制定了活動計劃,以下是活動計劃書的部分信息:
“讀書節”活動計劃書 | ||
書本類別 | A類 | B類 |
進價(單位:元) | 18 | 12 |
備注 | 1.用不超過16800元購進A,B兩類圖書共1000本; 2.A類圖書不少于600本; …… |
(1)陳經理查看計劃數時發現:A類圖書的標價是B類圖書標價的1.5倍,若顧客用540元購買圖書,能單獨購買A類圖書的數量恰好比單獨購買B類圖書的數量少10本,請求出A,B兩類圖書的標價;
(2)經市場調查后,陳經理發現他們高估了“讀書節”對圖書銷售的影響,便調整了銷售方案,A類圖書每本標價降低a元(0<a<5)銷售,B類圖書價格不變,那么書店應如何進貨才能獲得最大利潤?
查看答案和解析>>
科目:初中數學 來源: 題型:
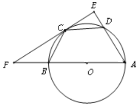
【題目】如圖,AB是⊙O的直徑,C,D在⊙O上,且BC=CD,過C作CE⊥AD,交AD延長線于E,交AB延長線于F點,
(1)求證:EF是⊙O的切線;
(2)若AB=4ED,求cos∠ABC的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
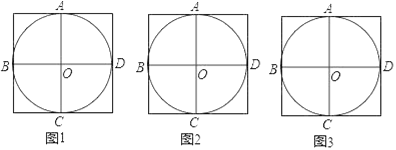
【題目】在圖1、2中,⊙O過了正方形網格中的格點A、B、C、D,請你僅用無刻度的直尺分別在圖1、圖2、圖3中畫出一個滿足下列條件的∠P
(1)頂點P在⊙O上且不與點A、B、C、D重合;
(2)∠P在圖1、圖2、圖3中的正切值分別為1、![]() 、2.
、2.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】光明中學全體學生900人參加社會實踐活動,從中隨機抽取50人的社會實踐活動成績制成如圖所示的條形統計圖,結合圖中所給信息解答下列問題:
![]() 填寫下表:
填寫下表:
中位數 | 眾數 | |
隨機抽取的50人的社會實踐活動成績 |
![]() 估計光明中學全體學生社會實踐活動成績的總分.
估計光明中學全體學生社會實踐活動成績的總分.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,把矩形紙片ABCD沿EF翻折,點A恰好落在BC邊的A′處,若AB= ![]() ,∠EFA=60°,則四邊形A′B′EF的周長是( )
,∠EFA=60°,則四邊形A′B′EF的周長是( )

A. 1+3![]() B. 3+
B. 3+![]() C. 4+
C. 4+![]() D. 5+
D. 5+![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com