
【題目】如圖,在△ABC中,AB=AC,AB的垂直平分線MN交AC于點D,交AB于點E.

(1)若∠A=50°,求∠DBC的度數.
(2)若AB=3,△CBD的周長為12,求△ABC得周長.
【答案】(1)15°;(2)15
【解析】
(1)根據等腰三角形內角和定理求出∠ABC=∠C=![]() (180°﹣∠A)=65°,根據線段垂直平分線的性質得出AD=BD,求出∠ABD=∠A=50°,即可求出答案;
(180°﹣∠A)=65°,根據線段垂直平分線的性質得出AD=BD,求出∠ABD=∠A=50°,即可求出答案;
(2)求出AD+DC+BC=AC+BC=15,即可求出答案.
解:(1)∵在△ABC中,AB=AC,∠A=50°,
∴∠ABC=∠C=![]() (180°﹣∠A)=65°,
(180°﹣∠A)=65°,
∵DE是AB的垂直平分線,
∴AD=BD,
∴∠ABD=∠A=50°,
∴∠DBC=∠ABC﹣∠ABD=65°﹣50°=15°;
(2)∵△CBD的周長為12,AD=BD,
∴BD+DC+BC=12,
∴AD+DC+BC=AC+BC=12,
∵AB=3,
∴△ABC的周長是AB+BC+AC=12+3=15


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】對于一個關于![]() 的代數式
的代數式![]() ,若存在一個系數為正數關于
,若存在一個系數為正數關于![]() 的單項式
的單項式![]() ,使
,使![]() 的結果是所有系數均為整數的整式,則稱單項式
的結果是所有系數均為整數的整式,則稱單項式![]() 為代數式
為代數式![]() 的“整系單項式” ,例如:
的“整系單項式” ,例如:
當![]() 時,由于
時,由于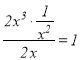 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于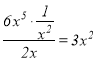 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于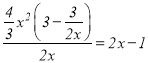 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
當![]() 時,由于
時,由于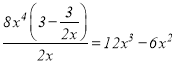 ,故
,故![]() 是
是![]() 的整系單項式;
的整系單項式;
顯然,當代數式![]() 存在整系單項式
存在整系單項式![]() 時,
時,![]() 有無數個,現把次數最低,系數最小的整系單項式
有無數個,現把次數最低,系數最小的整系單項式![]() 記為
記為![]() ,例如:
,例如:![]() .
.
閱讀以上材料并解決下列問題:
⑴.判斷:當![]() 時,
時,![]()
![]() 的整系單項式(填“是”或“不是”);
的整系單項式(填“是”或“不是”);
⑵.當![]() 時,
時,![]() = ;
= ;
⑶.解方程: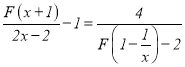 .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個工程隊同時參與一項工程建設,共同施工15天完成該項工程的![]() ,乙隊另有任務調走,甲隊又單獨施工30天完成了剩余的工程.
,乙隊另有任務調走,甲隊又單獨施工30天完成了剩余的工程.
(1)若乙隊單獨施工,需要多少天才能完成該項工程?
(2)若乙隊參與該項工程施工的時間不超過13天,則甲隊至少施工多少天才能完成該項工程?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AD⊥BC于點D,則下列四個結論中:
①線段AD上任意一點到點B的距離與到點C的距離相等;
②線段AD上任意一點到AB的距離與到AC的距離相等;
③若點Q是線段AD的三等分點 ,則△ACQ的面積是△ABC面積的![]() ;
;
④若![]() ,則
,則![]() ;
;
正確結論的序號是( )

A.①②③B.①②④C.①③④D.②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線y=![]() x﹣2分別交x、y軸于C、A,物線y=﹣
x﹣2分別交x、y軸于C、A,物線y=﹣![]() x2+
x2+![]() x﹣2經過A、C兩點,交x軸于另外一點B.點E為線段AC上一點,點F為線段AC延長線一點,AE=CF,點P為AC上方拋物線上的一點,當△PEF是以EF為底邊的等腰三角形,且tan∠PFE=
x﹣2經過A、C兩點,交x軸于另外一點B.點E為線段AC上一點,點F為線段AC延長線一點,AE=CF,點P為AC上方拋物線上的一點,當△PEF是以EF為底邊的等腰三角形,且tan∠PFE=![]() 時,求點P的坐標.
時,求點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知∠ABC=∠DCB,添加一個條件使△ABC≌△DCB,下列添加的條件不能使△ABC≌△DCB的是( )

A. ∠A=∠D B. AB=DC C. AC=DB D. OB=OC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】將一塊直角三角板DEF放置在銳角△ABC上,使得該三角板的兩條直角邊DE、DF恰好分別經過點B、C.

(1)如圖①,若∠A=40°時,點D在△ABC內,則∠ABC+∠ACB= 度,∠DBC+∠DCB= 度,∠ABD+∠ACD= 度;
(2)如圖②,改變直角三角板DEF的位置,使點D在△ABC內,請探究∠ABD+∠ACD與∠A之間存在怎樣的數量關系,并驗證你的結論.
(3)如圖③,改變直角三角板DEF的位置,使點D在△ABC外,且在AB邊的左側,直接寫出∠ABD、∠ACD、∠A三者之間存在的數量關系.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com