
【題目】在“植樹節”期間,小王、小李兩人想通過摸球的方式來決定誰去參加學校植樹活動,規則如下:在兩個盒子內分別裝入標有數字1,2,3,4的四個和標有數字1,2,3的三個完全相同的小球,分別從兩個盒子中各摸出一個球,如果所摸出的球上的數字之和小于6,那么小王去,否則就是小李去.
(1)用樹狀圖或列表法求出小王去的概率;
(2)小李說:“這種規則不公平”,你認同他的說法嗎?請說明理由.
 名牌學校分層周周測系列答案
名牌學校分層周周測系列答案 黃岡海淀全程培優測試卷系列答案
黃岡海淀全程培優測試卷系列答案科目:初中數學 來源: 題型:
【題目】如圖,已知∠B+∠BCD=180°,∠B=∠D.求證:∠E=∠DFE
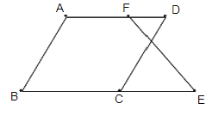
證明:∵∠B+∠BCD=180°(已知)
∴AB∥CD( )
∴∠B=∠DCE( )
又∵∠B=∠D(已知 ),
∴___________ (等量代換)
∴ ∥
∴∠E=∠DFE( )
查看答案和解析>>
科目:初中數學 來源: 題型:
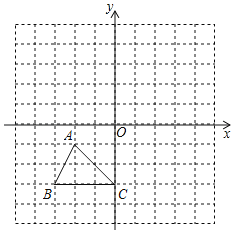
【題目】如圖,把三角形ABC向上平移4個單位長度,再向右平移3個單位長度,得到△A′B′C′.
(1)畫出△A′B′C′;并直接寫出點A′、B′、C′的坐標;
(2)若點P(m,n)是△ABC某邊上的點,經上述平移后,點P的對應點為P′,寫出點P′的坐標(用含m,n的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】教科書中這樣寫道:“我們把多項式![]() 及
及![]() 叫做完全平方式”,如果一個多項式不是完全平方式,我們常做如下變形:先添加一個適當的項,使式子中出現完全平方式,再減去這個項,使整個式子的值不變,這種方法叫做配方法.配方法是一種重要的解決問題的數學方法,不僅可以將一個看似不能分解的多項式分解因式,還能解決一些與非負數有關的問題或求代數式最大值,最小值等問題.
叫做完全平方式”,如果一個多項式不是完全平方式,我們常做如下變形:先添加一個適當的項,使式子中出現完全平方式,再減去這個項,使整個式子的值不變,這種方法叫做配方法.配方法是一種重要的解決問題的數學方法,不僅可以將一個看似不能分解的多項式分解因式,還能解決一些與非負數有關的問題或求代數式最大值,最小值等問題.
例如:分解因式![]() ;求代數式
;求代數式![]() 的最小值,
的最小值,![]() .可知當
.可知當![]() 時,
時,![]() 有最小值,最小值是
有最小值,最小值是![]() ,根據閱讀材料用配方法解決下列問題:
,根據閱讀材料用配方法解決下列問題:
(1)分解因式:![]() _______.
_______.
(2)當![]() 為何值時,多項式
為何值時,多項式![]() 有最大值?并求出這個最大值.
有最大值?并求出這個最大值.
(3)利用配方法,嘗試解方程![]() ,并求出
,并求出![]() ,
,![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
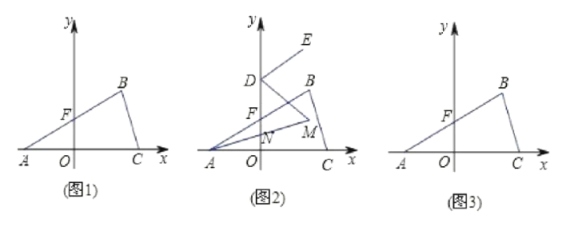
【題目】如(圖1),在平面直角坐標系中,![]() ,
,![]() ,
,![]() ,且滿足
,且滿足![]() ,線段
,線段![]() 交
交![]() 軸于
軸于![]() 點.
點.
(1)填空:![]() ,
,![]() ;
;
(2)點![]() 為
為![]() 軸正半軸上一點,若
軸正半軸上一點,若![]() ,
,![]() ,且
,且![]() 分別平分
分別平分![]() ,如(圖2),求
,如(圖2),求![]() 的度數;
的度數;
(3)求點![]() 的坐標;
的坐標;
(4)如(圖3),在![]() 軸上是否存在一點
軸上是否存在一點![]() ,使三角形
,使三角形![]() 的面積和三角形
的面積和三角形![]() 的面積相等?若存在,求出
的面積相等?若存在,求出![]() 點坐標,若不存在,說明理由.
點坐標,若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
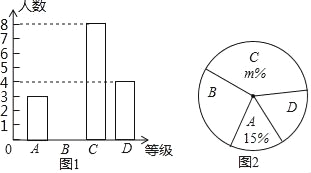
【題目】為了傳承中華民族優秀傳統文化,我市某中學舉行“漢字聽寫”比賽,賽后整理參賽學生的成績,將學生的成績分為A,B,C,D四個等級,并將結果繪制成圖1的條形統計圖和圖2扇形統計圖,但均不完整.請你根據統計圖解答下列問題:
(1)求參加比賽的學生共有多少名?并補全圖1的條形統計圖.
(2)在圖2扇形統計圖中,m的值為 ,表示“D等級”的扇形的圓心角為 度;
(3)組委會決定從本次比賽獲得A等級的學生中,選出2名去參加全市中學生“漢字聽寫”大賽.已知A等級學生中男生有1名,請用列表法或畫樹狀圖法求出所選2名學生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知方程組![]() 的解x為非正數,y為負數.
的解x為非正數,y為負數.
(1)求a的取值范圍;
(2)化簡∣a-3∣+∣a+2∣;
(3)在a的取值范圍內,m是最大的整數,n是最小的整數,求(m+n)m-n的值;
(4)在a的取值范圍內,當a取何整數時,不等式2ax+x>2a+1的解為x<1.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在△ABC中,AB=BC=10,以AB為直徑作⊙O分別交AC,BC于點D,E,連接DE和DB,過點E作EF⊥AB,垂足為F,交BD于點P.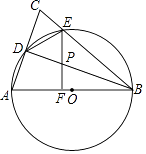
(1)求證:AD=DE;
(2)若CE=2,求線段CD的長;
(3)在(2)的條件下,求△DPE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4,BC=6,將矩形ABCD繞B逆時針旋轉30°后得到矩形GBEF,延長DA交FG于點H,則GH的長為( )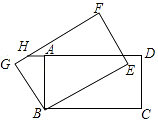
A.8﹣4 ![]()
B.![]() ﹣4
﹣4
C.3 ![]() ﹣4
﹣4
D.6﹣3 ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com