
【題目】某學校為了推動球類運動的普及,成立多個球類運動社團,為此,學生會采取抽樣調查的方法,從足球、乒乓球、籃球、排球四個項目調查了若干名學生的興趣愛好(要求每位同學只能選擇其中一種自己喜歡的球類運動),并將調查結果繪制成了如下條形統計圖和扇形統計圖(不完整).請你根據圖中提供的信息,解答下列問題:

(1)本次抽樣調查,共調查了 名學生;
(2)請將條形統計圖和扇形統計圖補充完整;
(3)若該學校共有學生1800人,根據以上數據分析,試估計選擇排球運動的同學約有多少人?
【答案】(1)400;(2)見解析;(3)180.
【解析】
試題(1)根據喜歡足球的人數與所占的百分比列式計算即可求出調查的學生總人數;
(2)分別計算出乒乓球、籃球的人數、籃球所占的百分比、排球所占的百分比,即可補全統計圖;
(3)用1800×選擇排球運動的百分比,即可解答
試題解析:(1)100÷25%=400(人),
∴本次抽樣調查,共調查了400名學生;
故答案為:400.
(2)乒乓球的人數:400×40%=160(人),籃球的人數:400﹣100﹣160﹣40=100(人),
籃球所占的百分比為:![]() =25%,排球所占的百分比為:
=25%,排球所占的百分比為:![]() ×100%=10%,
×100%=10%,
如圖所示:

(3)1800×10%=180(人),
∴若該學校共有學生1800人,根據以上數據分析,試估計選擇排球運動的同學約有180人.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】用火柴棒按下圖的方式搭塔式三角形,第一個圖用了3根火柴棒,第二個圖用了9根火柴棒,第三個圖用了18根火柴棒,......,照這樣下去,第9個圖用了_____根火柴棒.
 ……
……
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】△ABC在直角坐標系中的位置如圖所示,其中A(﹣3,5),B(﹣5,2),C(﹣1,3),直線l經過點(0,1),并且與x軸平行,△A′B′C′與△ABC關于線1對稱.
(1)畫出△A′B′C′,并寫出△A′B′C′三個頂點的坐標: ;
(2)觀察圖中對應點坐標之間的關系,寫出點P(a,b)關于直線l的對稱點P′的坐標: ;
(3)若直線l′經過點(0,m),并且與x軸平行,根據上面研究的經驗,寫出點Q(c,d)關于直線1′的對稱點Q′的坐標: .

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在直角坐標系xOy中,點A,B分別在x軸和y軸上, ![]() =
= ![]() ,∠AOB的角平分線與OA的垂直平分線交于點C,與AB交于點D,反比例函數y=
,∠AOB的角平分線與OA的垂直平分線交于點C,與AB交于點D,反比例函數y= ![]() 的圖象過點C,若以CD為邊的正方形的面積等于
的圖象過點C,若以CD為邊的正方形的面積等于 ![]() ,則k的值是.
,則k的值是.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AD是△ABC的角平分線,DF⊥AB,垂足為F,DE=DG,△ADG和△AED的面積分別為25和17,則△EDF的面積為( )

A. 4 B. 5 C. 5.5 D. 6
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖是一個玩具火車軌道,點A有個變軌開關,可以連接點B或點C.小圈軌道的周長是2米,大圈軌道的周長是4米.開始時,點A連接點C,火車從點A出發,按照順時針方向在軌道上移動,同時變軌開關每隔一分鐘變換一次軌道連接.若火車的速度是每分鐘10米,則火車第10次回到A點時用了 分鐘.
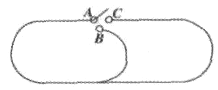
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直線AB、CD相交于點O.已知∠BOD=75°,OE把∠AOC分成兩個角,且∠AOE:∠EOC=2:3.
(1)求∠AOE的度數;
(2)若OF平分∠BOE,問:OB是∠DOF的平分線嗎?試說明理由.
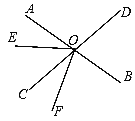
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com