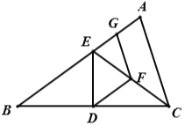
【題目】如圖，
中，
是
的垂直平分線，
是
的平分線，
為
的中位線，連
，若
，則
_______
【答案】126°
【解析】
利用垂直平分線得到∠EBC=∠ECB=x，再利用外角與中位線性質，求出x的值，再根據
∠AEC+∠CED=2x+90-x=90+x求出答案．
解：
DE是BC的垂直平分線
BE=CE
設∠EBC=∠ECB=x
∴∠AEC=∠EBC+∠ECB=2x
∵CE平分∠ACB
∴∠BCE=∠ACE=x
∵FG為
的中位線
∴FG//AC
∴∠EFG=∠ACE=x
∵D為BC中點，F為CE中點
∴DF//AB
∴∠EFD=∠AEF=2x
∵∠DFG=∠GFE+∠EFD=x+2x=3x
∴3x=108
∴x=36
∴∠AED=∠AEC+∠CED=2x+90-x=90+x=90+36=126．
故答案為：126度．
七彩題卡口算應用一點通系列答案科目：初中數學 來源： 題型：
【題目】已知拋物線
，
，
，…，
（n為正整數），點A(0，1)．
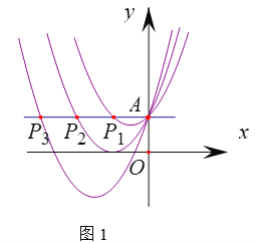
（1）如圖1，過點A作y軸垂線，分別交拋物線
，
，
，…，
于點
，
，
，…，
（和點A不重合）．
①求
的長．
②求
的長．
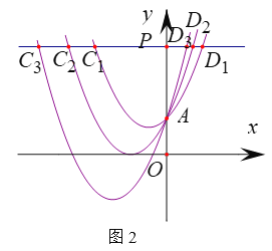
（2）如圖2，點P從點A出發，沿y軸向上運動，過點P作y軸的垂線，交拋物線于點
，
，交拋物線于點
，
，交拋物線于點
，
，……，交拋物線于點
，
（在第二象限）．
①求
的值．
②求
的值．
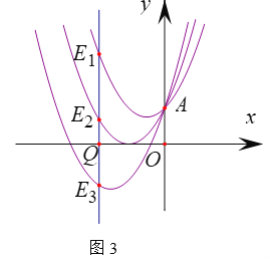
（3）過x軸上的點Q（原點除外），作x軸的垂線分別交拋物線，，，…，于點
，
，
，…，
，是否存在線段
（i，j為正整數），使
，若存在，求出i＋j的最小值；若不存在，說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】定義：如果將△ABC與△DEF各分割成兩個三角形，且△ABC所分的兩個三角形與△DEF所分的兩個三角形分別對應相似，那么稱△ABC與△DEF互為“近似三角形”，將每條分割線稱為“近似分割線”．
（1）如圖1，在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，∠A＝30°，∠D＝40°，請判斷這兩個三角形是否互為“近似三角形”？如果是，請直接在圖1中畫出一組分割線，并注明分割后所得兩個小三角形銳角的度數；若不是，請說明理由．
（2）判斷下列命題是真命題還是假命題，若是真命題，請在括號內打“√”；若是假命題，請在括號內打“×”．
①任意兩個直角三角形都是互為“近似三角形” ；
②兩個“近似三角形”只有唯一的“近似分割線” ；
③如果兩個三角形中有一個角相等，那么這兩個三角形一定是互為“近似三角形” ．
（3）如圖2，已知△ABC與△DEF中，∠A＝∠D＝15°，∠B＝45°，∠E＝60°，且BC＝EF＝
，判斷這兩個三角形是否互為“近似三角形”？如果是，請在圖2中畫出不同位置的“近似分割線”，并直接分別寫出“近似分割線”的和；如果不是，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
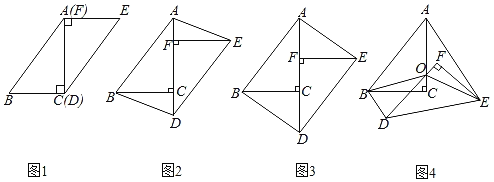
【題目】在一次數學研究性學習中，小兵將兩個全等的直角三角形紙片ABC和DEF拼在一起，使點A與點F重合，點C與點D重合（如圖1），其中∠ACB＝∠DFE＝90°，BC＝EF＝3cm，AC＝DF＝4cm，并進行如下研究活動．
活動一：將圖1中的紙片DEF沿AC方向平移，連結AE，BD（如圖2），當點F與點C重合時停止平移．
（思考）圖2中的四邊形ABDE是平行四邊形嗎？請說明理由．
（發現）當紙片DEF平移到某一位置時，小兵發現四邊形ABDE為矩形（如圖3）．求AF的長．
活動二：在圖3中，取AD的中點O，再將紙片DEF繞點O順時針方向旋轉α度（0≤α≤90），連結OB，OE（如圖4）．
（探究）當EF平分∠AEO時，探究OF與BD的數量關系，并說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】每年的3月15日是“國際消費者權益日”，許多家居商城都會利用這個契機進行打折促銷活動.甲賣家的某款沙發每套成本為5000元，在標價8000元的基礎上打9折銷售.
（1）現在甲賣家欲繼續降價吸引買主，問最多降價多少元，才能使利潤率不低于20%？
（2）據媒體爆料，有一些賣家先提高商品價格后再降價促銷，存在欺詐行為.乙賣家也銷售相同的沙發，其成本、標價與甲賣家一致，以前每周可售出8套，現乙賣家先將標價提高
，再大幅降價
元，使得這款沙發在3月15日那一天賣出的數量就比原來一周賣出的數量增加了
，這樣一天的利潤達到了50000元，求
的值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某大學生利用40天社會實踐參與了某加盟店經營，他銷售了一種成本為20元/件的商品，細心的他發現在第
天銷售的相關數據可近似地用如下表中的函數表示：
銷售量 | 銷售單價 | |
| 當 | 當 |
（1）求前20天第幾天獲得的利潤最大？最大利潤是多少？
（2）求后20天第幾天獲得的利潤最大？最大利潤是多少？
（3）在后20天中，他決定每銷售一件商品給山區孩子捐款
元（
且為整數），此時若還要求每一天的利潤都不低于160元，求的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，矩形EFGH的頂點E，G分別在菱形ABCD的邊AD，BC上，頂點F，H在菱形ABCD的對角線BD上．
（1）求證：BG=DE；
（2）若E為AD中點，FH=2，求菱形ABCD的周長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】珠海市有A，B，C，D，E五個景區很受游客喜愛．對某小區居民在暑假期間去以上五個景區旅游（只選一個景區）的意向做了一次隨機調查統計，并根據這個統計結果制作了如下兩幅不完整的統計圖．
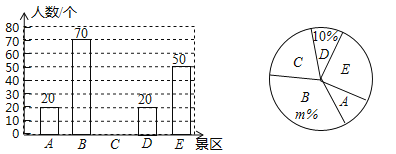
（1）該小區居民在這次隨機調查中被調查到的人數是 人，m＝ ；
（2）若該小區有居民1500人，試估計去C景區旅游的居民約有多少人？
（3）甲、乙兩人暑假打算游玩，甲從B、C兩個景點中任意選擇一個游玩，乙從B、C 、E三個景點中任意選擇一個游玩．求甲、乙恰好游玩同一景點的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為阻斷新冠疫情向校園蔓延，確保師生生命安全和身體健康，教育部通知，2020年春季學期延期開學，利用網上平臺，停課不停學”，某校對初三全體學生數學線上學習情況進行調查，隨機抽取部分學生的4月月診斷性測試成績，按由高到低分為A，B，C，D四個等級，根據調查的數據繪制成如下的條形統計圖和扇形統計圖，請根據圖中的信息，解答下列問題：
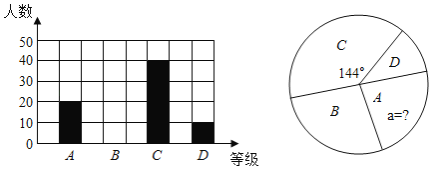
(1)該校共抽查了 名同學的數學測試成績，扇形統計圖中A等級所占的百分比a＝ ；
(2)補全條形統計圖；
(3)若該校初三共有1180名同學，請估計該校初三學生數學測試成績優秀（測試成績B級以上為優秀，含B級）約有 名；
(4)該校老師想從兩男、兩女四位學生中隨機選擇兩位了解平時線上學習情況，請用列表或畫樹形圖的方法求出恰好選中一男一女的概率．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
