【題目】如圖，直線
經過點
且與直線
交于點
．
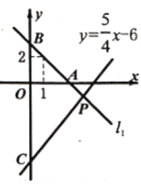
(1)求點
的坐標．
(2)求直線的表達式．
(3)若直線與
軸、
軸分別交于
兩點，直線與軸交于點
， 求
的面積．
【答案】（1）點P坐標為（4，-1）；（2）直線l1的表達式為y=-x+3；（3）△PBC的面積為18．
【解析】
（1）把點P坐標代入直線
，即可求解；
（2）設直線l1的表達式為
，根據直線經過點（1，2）和（4，-1），待定系數法即可求解；
（3）分別求出點B、C坐標，求出BC，根據三角形面積公式計算即可．
解：（1）把點
代入直線，得：
，
∴a=4，
∴點P坐標為（4，-1），
（2）設直線l1的表達式為，
∵直線經過點（1，2）和（4，-1），
∴
，
解得：
，
∴直線l1的表達式為y=-x+3；
（3）∵直線y=-x+3和分別與y軸交于點B和點C，
∴點B坐標為（0，3），點C坐標為（0，-6），
∴BC=9 ，
∵點P坐標為（4，-1），
∴△PBC的面積為：
=18．
閱讀快車系列答案科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中點A的坐標為(0，6)，點B的坐標為(﹣
，5)，將△AOB沿x軸向左平移得到△A′O′B′，點A的對應點A′落在直線y＝﹣
x上，則點B的對應點B′的坐標為（ ）
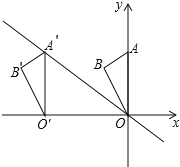
A.(﹣8，6)B.(﹣
，5)C.(﹣
，5)D.(﹣8，5)
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，二次函數y=（x+2）2+m的圖象與y軸交于點C，點B在拋物線上，且與點C關于拋物線的對稱軸對稱，已知一次函數y=kx+b的圖象經過該二次函數圖象上的點A（﹣1，0）及點B．
（1）求二次函數與一次函數的解析式；
（2）根據圖象，寫出滿足（x+2）2+m≥kx+b的x的取值范圍．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC 中，點O是AC邊上的一個動點，過點O作直線MN∥BC，設MN交∠BCA的角平分線于點E，交∠BCA的外角平分線于點F
（1）求證：EO=FO；
（2）當點O運動到何處時，四邊形AECF是矩形？并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】在探究一次函數
的圖像性質時我們有如下發現：
①系數
決定了函數圖像的坡度，
越大則圖像坡度越大(越靠近
軸)，越小則圖像坡度越小(越靠近
軸)；
②常數項
決定了圖像與軸的交點，即函數圖像與軸交點坐標始終為
．
基于以上發現，我們得出結論：如果兩個一次函數的值相同，那么兩個一次函數的圖像平行.反之，如果兩直線平行，則兩條直線所對應的函數表達式的值一定相等：把函數圖像沿軸向上(或向下) 平移
個單位， 系數保持不變， 常數變為
(或
).如：函數
和
的圖像互相平行：函數
的圖像向上平移2個單位后所得函數表達式為
．
據此回答下列問題：
(1) 把函數
的圖像向上平移4個單位后所得函數的表達式為____；
(2)把函數
的圖像向 (上或下)平移 個單位可得到函數
的圖像；
(3)若直線經過點
且與直線
平行，求出直線的表達式．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，數軸上有A、B兩點．
（1）分別寫出A、B兩點表示的數： 、 ；
（2）若點C表示﹣0.5，把點C表示在如圖所示的數軸上；
（3）將點B向左移動3個單位長度，得到點D，點A、B、C、D所表示的四個數用“＜”連接的結果： ．
查看答案和解析>>
科目：初中數學 來源： 題型：
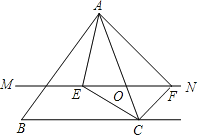
【題目】如圖，在△ABC中，點O是AC邊上（端點除外）的一個動點，過點O作直線MN∥BC．設MN交∠BCA的平分線于點E，交∠BCA的外角平分線于點F，連接AE、AF．那么當點O運動到何處時，四邊形AECF是矩形？并證明你的結論．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】兩塊完全相同的三角板Ⅰ（△ABC）和Ⅱ（△A1B1C1）如圖①放置在同一平面上（∠C=∠C1=90°，∠ABC=∠A1B1C1=60°），斜邊重合．若三角板Ⅱ不動，三角板Ⅰ在三角板Ⅱ所在的平面上向右滑動，圖②是滑動過程中的一個位置．
（1）在圖②中，連接BC1、B1C，求證：△A1BC1≌△AB1C；
（2）三角板Ⅰ滑到什么位置（點B1落在AB邊的什么位置）時，四邊形BCB1C1是菱形？說明理由．
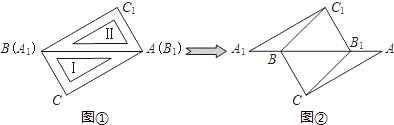
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
