
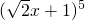 的運算可以轉化為五個多項式
的運算可以轉化為五個多項式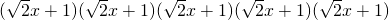 相乘,按多項式乘法法則,展開合并同類項后其乘積為:a5x5+a4x4+a3x3+a2x2+a1x+a0,其中a5、a4、a3、a2、a1、a0為乘積展開式各項的系數,因此,
相乘,按多項式乘法法則,展開合并同類項后其乘積為:a5x5+a4x4+a3x3+a2x2+a1x+a0,其中a5、a4、a3、a2、a1、a0為乘積展開式各項的系數,因此,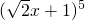 =a5x5+a4x4+a3x3+a2x2+a1x+a0.
=a5x5+a4x4+a3x3+a2x2+a1x+a0. x+1)5=a5x5+a4x4+a3x3+a2x2+a1x+a0,
x+1)5=a5x5+a4x4+a3x3+a2x2+a1x+a0, )5=4
)5=4 .
. x+1)5=a5x5+a4x4+a3x3+a2x2+a1x+a0在上述等式中:
x+1)5=a5x5+a4x4+a3x3+a2x2+a1x+a0在上述等式中: +1)5=a5+a4+a3+a2+a1+a0,
+1)5=a5+a4+a3+a2+a1+a0, +1)5=-a5+a4-a3+a2-a1+a0,
+1)5=-a5+a4-a3+a2-a1+a0, +1)5(-
+1)5(- +1)5,
+1)5, +1)5=a5+a4+a3+a2+a1+a0①
+1)5=a5+a4+a3+a2+a1+a0① +1)5=-a5+a4-a3+a2-a1+a0②
+1)5=-a5+a4-a3+a2-a1+a0②

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
查看答案和解析>>
科目:初中數學 來源:2007年湖北省武漢市黃陂一中分配生素質測試數學試卷(解析版) 題型:解答題
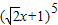 的運算可以轉化為五個多項式
的運算可以轉化為五個多項式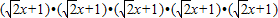 相乘,按多項式乘法法則,展開合并同類項后其乘積為:a5x5+a4x4+a3x3+a2x2+a1x+a,其中a5、a4、a3、a2、a1、a為乘積展開式各項的系數,因此,
相乘,按多項式乘法法則,展開合并同類項后其乘積為:a5x5+a4x4+a3x3+a2x2+a1x+a,其中a5、a4、a3、a2、a1、a為乘積展開式各項的系數,因此, =a5x5+a4x4+a3x3+a2x2+a1x+a.
=a5x5+a4x4+a3x3+a2x2+a1x+a.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com