
 ,
,
 ,
,
 ,
, ,
,

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:

| 5 | 6 |
查看答案和解析>>
科目:初中數學 來源: 題型:
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
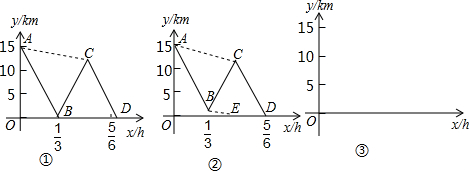
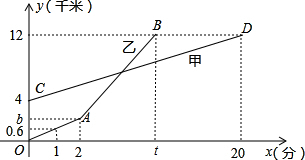
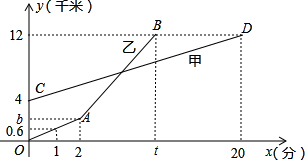
 h.圖②中折線A-B-C-D、線段AC、線段BE分別表示王老師、甲、乙在上述過程中,離車站的路程y(km)與王老師所用時間x(h)之間的函數關系.求a的值.
h.圖②中折線A-B-C-D、線段AC、線段BE分別表示王老師、甲、乙在上述過程中,離車站的路程y(km)與王老師所用時間x(h)之間的函數關系.求a的值.查看答案和解析>>
科目:初中數學 來源:2013年江蘇省南京市白下區中考數學一模試卷(解析版) 題型:解答題
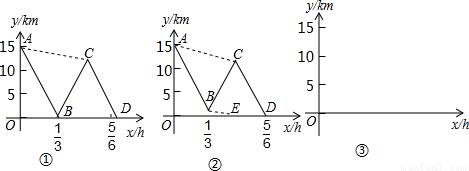
 h.圖②中折線A-B-C-D、線段AC、線段BE分別表示王老師、甲、乙在上述過程中,離車站的路程y(km)與王老師所用時間x(h)之間的函數關系.求a的值.
h.圖②中折線A-B-C-D、線段AC、線段BE分別表示王老師、甲、乙在上述過程中,離車站的路程y(km)與王老師所用時間x(h)之間的函數關系.求a的值.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com