
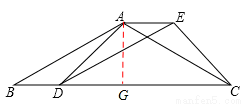
如圖,已知四邊形ABDE是平行四邊形,C為邊B D延長線上一點,連結AC、CE,使AB=AC.

(1)求證:△BAD≌△AEC;
(2)若∠B=30°,∠ADC=45°,BD=10,求平行四邊形ABDE的面積.
解:(1)證明:∵AB=AC, ∴∠B=∠ACB.
又∵四邊形ABDE是平行四邊形,∴AE∥BD,AE=BD。
∴∠ACB=∠CAE=∠B。
在△DBA和△AEC中,∵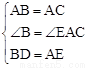 ,∴△DBA≌△AEC(SAS)。
,∴△DBA≌△AEC(SAS)。
(2)過A作AG⊥BC,垂足為G。設AG=x,
在Rt△AGD中,∵∠ADC=45°,∴AG=DG=x。
在Rt△AGB中,∵∠B=30°,∴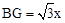 。
。
又∵BD=10,
∴BG-DG=BD,即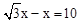 ,解得
,解得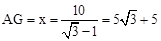 。
。
∴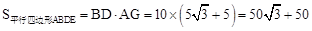
【解析】
試題分析:(1)應用平行四邊形的性質由SAS證明△DBA≌△AEC。
(2)過A作AG⊥BC,垂足為G,設AG=x,首先根據銳角三角函數關系得出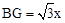 ,進而利用BG-DG=BD求出AG的長,進而得出平行四邊形ABDE的面積。
,進而利用BG-DG=BD求出AG的長,進而得出平行四邊形ABDE的面積。


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
 |
| BDC |
 的延長線分別交于點F、E,且
的延長線分別交于點F、E,且 |
| BF |
 |
| AD |
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com