
【題目】如圖,在四邊形![]() 中,
中,![]() ,頂點
,頂點![]() 是原點,頂點
是原點,頂點![]() 在
在![]() 軸上,頂點
軸上,頂點![]() 的坐標為
的坐標為![]() ,
,![]() ,
,![]() ,點
,點![]() 從點
從點![]() 出發,以
出發,以![]() 的速度向點
的速度向點![]() 運動,點
運動,點![]() 從點
從點![]() 同時出發,以
同時出發,以![]() 的速度向點
的速度向點![]() 運動.規定其中一個動點到達端點時,另一個動點也隨之停止運動;從運動開始,設
運動.規定其中一個動點到達端點時,另一個動點也隨之停止運動;從運動開始,設![]() 點運動的時間為
點運動的時間為![]() .
.
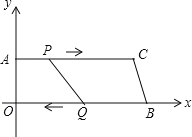
![]() 求直線
求直線![]() 的函數解析式;
的函數解析式;
![]() 當
當![]() 為何值時,四邊形
為何值時,四邊形![]() 是矩形?
是矩形?
 星級口算天天練系列答案
星級口算天天練系列答案 芒果教輔達標測試卷系列答案
芒果教輔達標測試卷系列答案科目:初中數學 來源: 題型:
【題目】一輛慢車和一輛快車沿相同路線從A地到B地,所行駛的路程與時間的函數圖象如圖所示,下列說法正確的有()個
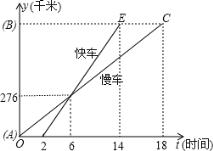
①快車追上慢車需6小時
②慢車比快車早出發2小時
③快車速度為46km/h
④慢車速度為46km/h
⑤AB兩地相距828km
⑥快車14小時到達B地
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位線,點M是邊BC上一點,BM=3,點N是線段MC上的一個動點,連接DN,ME,DN與ME相交于點O.若△OMN是直角三角形,則DO的長是______.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于平面直角坐標系xOy中的圖形M,N,給出如下定義:P為圖形M上任意一點,Q為圖形N上任意一點,如果P,Q兩點間的距離有最小值,那么稱這個最小值為圖形M,N間的"距離",記作d(M,N) . 特別的,當圖形M,N有公共點時,記作d(M,N)=0.一次函數y=kx+2的圖像為L,L 與y 軸交點為D, △ABC中,A(0,1),B(-1,0),C(1,0).
(1)求d(點 D , △ABC)= ;當k=1時,求d( L , △ABC)= ;
(2)若d(L, △ABC)=0.直接寫出k的取值范圍;
(3)函數y=x+b的圖像記為W , 若d(W,△ABC) ![]() 1 ,求出b的取值范圍.
1 ,求出b的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了加強公民的節水意識,合理利用水資源,各地采取價格調控手段達到節約用水的目的,某市規定如下用水收費標準:每戶每月的用水量不超過![]() 立方米時,水費按每立方米
立方米時,水費按每立方米![]() 元收費,超過
元收費,超過![]() 立方米時,不超過的部分每立方米仍按
立方米時,不超過的部分每立方米仍按![]() 元收費,超過的部分每立方米按
元收費,超過的部分每立方米按![]() 元收費,該市某戶今年
元收費,該市某戶今年![]() 月份的用水量和所交水費如下表所示:
月份的用水量和所交水費如下表所示:
月份 | 用水量( | 收費(元) |
|
|
|
|
|
|
設某戶每月用水量![]() (立方米),應交水費
(立方米),應交水費![]() (元)
(元)
![]() 求
求![]() 的值,當
的值,當![]() 時,分別寫出
時,分別寫出![]() 與
與![]() 的函數關系式.
的函數關系式.
![]() 若該戶
若該戶![]() 月份用水量為
月份用水量為![]() 立方米,求該
立方米,求該![]() 月份水費多少元?
月份水費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
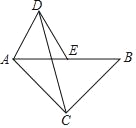
【題目】如圖,在等腰Rt△ABC中,∠ACB=90°,AB=4,點E為AB的中點.以AE為邊作等邊△ADE(點D與點C分別在AB的異側),連接CD.則△ACD的面積為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖1,點M為直線AB上一動點,△PAB,△PMN都是等邊三角形,連接BN,

(1)求證:AM=BN;
(2)寫出點M在如圖2所示位置時,線段AB、BM、BN三者之間的數量關系,并給出證明;
(3)點M在圖3所示位置時,直接寫出線段AB、BM、BN三者之間的數量關系.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】計算:
(1)(﹣8)﹣(﹣15)+(﹣9)﹣(﹣12)
(2)7![]() +(﹣6.5)+3
+(﹣6.5)+3![]() +(﹣1.25)+2
+(﹣1.25)+2![]()
(3)(﹣81)÷(﹣2![]() )×
)×![]() ÷(﹣8)
÷(﹣8)
(4)![]()
(5)![]()
(6)![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小張和同學相約“五一”節到離家2400米的電影院看電影,到電影院后,發現電影票忘帶了,此時離電影開始還有25分鐘,于是他跑步回家,拿到票后立刻找到一輛“共享單車”原路趕回電影院,已知小張騎車的時間比跑步的時間少用了4分鐘,騎車的平均速度是跑步的平均速度的1.5倍.
(1)求小張跑步的平均速度;
(2)如果小張在家取票和尋找“共享單車”共用了6分鐘,他能否在電影開始前趕到電影院?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com