
【題目】2020年是全面建成小康社會收官之年,某扶貧幫扶小組積極響應(yīng),對農(nóng)民實(shí)施精準(zhǔn)扶貧.某農(nóng)戶老張家種植花椒和黑木耳兩種干貨共800千克,扶貧小組通過市場調(diào)研發(fā)現(xiàn),花椒市場價(jià)60元/千克,黑木耳市場價(jià)48元/千克,老張全部售完可以收入4.2萬元.已知老張種植花椒成本需25元/千克,種植木耳成本需35元/千克,根據(jù)脫貧目標(biāo)任務(wù)要求,老張種植花椒和黑木耳的兩種干貨的純收入(銷售收入-種植成本)在2萬元以上才可以順利脫貧.請你分析一下扶貧幫扶小組是否能幫助老張順利脫貧.
 備戰(zhàn)中考寒假系列答案
備戰(zhàn)中考寒假系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
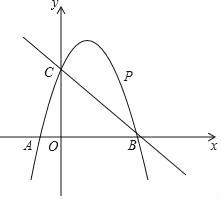
【題目】如圖,已知二次函數(shù)y=ax2+2x+c的圖象經(jīng)過點(diǎn)C(0,3),與x軸分別交于點(diǎn)A,點(diǎn)B(3,0).點(diǎn)P是直線BC上方的拋物線上一動點(diǎn).
(1)求二次函數(shù)y=ax2+2x+c的表達(dá)式;
(2)連接PO,PC,并把△POC沿y軸翻折,得到四邊形POP′C.若四邊形POP′C為菱形,請求出此時點(diǎn)P的坐標(biāo);
(3)當(dāng)點(diǎn)P運(yùn)動到什么位置時,四邊形ACPB的面積最大?求出此時P點(diǎn)的坐標(biāo)和四邊形ACPB的最大面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,四邊形![]() 是矩形,點(diǎn)
是矩形,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() .點(diǎn)
.點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿
出發(fā),沿![]() 以每秒1個單位長度的速度向點(diǎn)
以每秒1個單位長度的速度向點(diǎn)![]() 運(yùn)動,同時點(diǎn)
運(yùn)動,同時點(diǎn)![]() 從點(diǎn)
從點(diǎn)![]() 出發(fā),沿
出發(fā),沿![]() 以每秒2個單位長度的速度向點(diǎn)
以每秒2個單位長度的速度向點(diǎn)![]() 運(yùn)動,當(dāng)點(diǎn)
運(yùn)動,當(dāng)點(diǎn)![]() 與點(diǎn)
與點(diǎn)![]() 重合時運(yùn)動停止.設(shè)運(yùn)動時間為
重合時運(yùn)動停止.設(shè)運(yùn)動時間為![]() 秒.
秒.
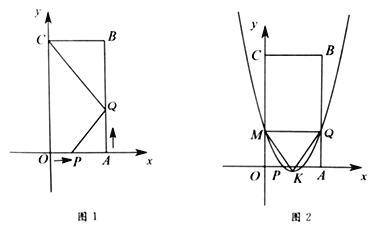
(1)當(dāng)![]() 時,線段
時,線段![]() 的中點(diǎn)坐標(biāo)為________;
的中點(diǎn)坐標(biāo)為________;
(2)當(dāng)![]() 與
與![]() 相似時,求
相似時,求![]() 的值;
的值;
(3)當(dāng)![]() 時,拋物線
時,拋物線![]() 經(jīng)過
經(jīng)過![]() 、
、![]() 兩點(diǎn),與
兩點(diǎn),與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,拋物線的頂點(diǎn)為
,拋物線的頂點(diǎn)為![]() ,如圖2所示.問該拋物線上是否存在點(diǎn)
,如圖2所示.問該拋物線上是否存在點(diǎn)![]() ,使
,使![]() ,若存在,求出所有滿足條件的
,若存在,求出所有滿足條件的![]() 點(diǎn)坐標(biāo);若不存在,說明理由.
點(diǎn)坐標(biāo);若不存在,說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
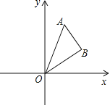
【題目】如圖,在平面直角坐標(biāo)系![]() 中,點(diǎn)
中,點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,將
,將![]() 繞著點(diǎn)
繞著點(diǎn)![]() 旋轉(zhuǎn)
旋轉(zhuǎn)![]() 后得到
后得到![]() .
.
![]() 在圖中畫出
在圖中畫出![]() ;
;
![]() 點(diǎn)
點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() 的對應(yīng)點(diǎn)
的對應(yīng)點(diǎn)![]() ’和
’和![]() ’的坐標(biāo)分別是
’的坐標(biāo)分別是![]() ’________和
’________和![]() ’________;
’________;
![]() 請直接寫出
請直接寫出![]() 和
和![]() ’
’![]() ’的數(shù)量關(guān)系和位置關(guān)系.
’的數(shù)量關(guān)系和位置關(guān)系.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
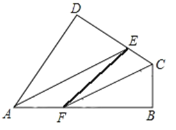
【題目】如圖,已知四邊形ABCD中,∠D=∠B=90°,AE平分∠DAB,CF平分∠DCB.試判斷∠AEF與∠CFE是否相等?并證明你的結(jié)論.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】(綜合與實(shí)踐
如圖,直線![]() 的函數(shù)關(guān)系式為
的函數(shù)關(guān)系式為![]() ,且
,且![]() 與
與![]() 軸交于點(diǎn)A,直線
軸交于點(diǎn)A,直線![]() 經(jīng)過點(diǎn)B(2,0),C(-1,3),直線
經(jīng)過點(diǎn)B(2,0),C(-1,3),直線![]() 與
與![]() 交于點(diǎn)D.
交于點(diǎn)D.
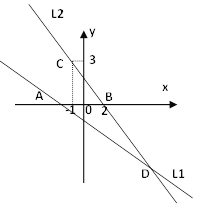
(1)求直線![]() 的函數(shù)關(guān)系式;
的函數(shù)關(guān)系式;
(2)求△ABD的面積.
(3)點(diǎn)P是![]() 軸上一動點(diǎn),問是否存在一點(diǎn)P,恰好使△ADP為直角三角形?若存在,直接寫出點(diǎn)P的坐標(biāo);若不存在,請說明理由.
軸上一動點(diǎn),問是否存在一點(diǎn)P,恰好使△ADP為直角三角形?若存在,直接寫出點(diǎn)P的坐標(biāo);若不存在,請說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,已知直線![]() 的同側(cè)有兩個點(diǎn)
的同側(cè)有兩個點(diǎn)![]() 、
、![]() ,在直線
,在直線![]() 上找一點(diǎn)
上找一點(diǎn)![]() ,使
,使![]() 點(diǎn)到
點(diǎn)到![]() 、
、![]() 兩點(diǎn)的距離之和最短的問題,可以通過軸對稱來確定,即作出其中一點(diǎn)關(guān)于直線
兩點(diǎn)的距離之和最短的問題,可以通過軸對稱來確定,即作出其中一點(diǎn)關(guān)于直線![]() 的對稱點(diǎn),對稱點(diǎn)與另一點(diǎn)的連線與直線
的對稱點(diǎn),對稱點(diǎn)與另一點(diǎn)的連線與直線![]() 的交點(diǎn)就是所要找的點(diǎn),通過這種方法可以求解很多問題.
的交點(diǎn)就是所要找的點(diǎn),通過這種方法可以求解很多問題.
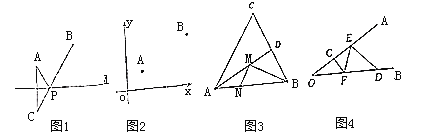
(1)如圖2,在平面直角坐標(biāo)系內(nèi),點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,點(diǎn)
,點(diǎn)![]() 的坐標(biāo)為
的坐標(biāo)為![]() ,動點(diǎn)
,動點(diǎn)![]() 在
在![]() 軸上,求
軸上,求![]() 的最小值;
的最小值;
(2)如圖3,在銳角三角形![]() 中,
中,![]() ,
,![]() ,
,![]() 的角平分線交
的角平分線交![]() 于點(diǎn)
于點(diǎn)![]() ,
,![]() 、
、![]() 分別是
分別是![]() 和
和![]() 上的動點(diǎn),則
上的動點(diǎn),則![]() 的最小值為______.
的最小值為______.
(3)如圖4,![]() ,
,![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() ,
,![]() 分別是射線
分別是射線![]() ,
,![]() 上的動點(diǎn),則
上的動點(diǎn),則![]() 的最小值為__________.
的最小值為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
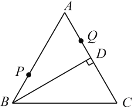
【題目】如圖,等邊△![]() 中,
中,![]() 于
于![]() ,
,![]() ,點(diǎn)
,點(diǎn)![]() 、
、![]() 分別為
分別為![]() 、
、![]() 上的兩個定點(diǎn)且
上的兩個定點(diǎn)且![]() ,在
,在![]() 上有一動點(diǎn)
上有一動點(diǎn)![]() 使
使![]() 最短,則
最短,則![]() 的最小值為_____
的最小值為_____![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com