
 平面直角坐標系內有兩條直線l1、l2,直線l1的解析式為
平面直角坐標系內有兩條直線l1、l2,直線l1的解析式為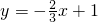 ,如果將坐標紙折疊,使直線l1與l2重合,此時點(-2,0)與點(0,2)也重合.
,如果將坐標紙折疊,使直線l1與l2重合,此時點(-2,0)與點(0,2)也重合.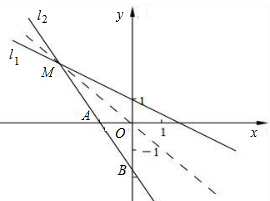 解:如圖所示:
解:如圖所示: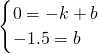 ,
,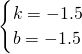 ;
; =
= ;
; ;
;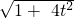 ?t=0或t=
?t=0或t= ,
, t,
t,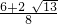 或t=
或t=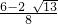 (舍去),a=
(舍去),a=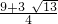 ,b=-
,b=-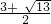 ;
;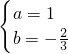 或
或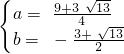 .
.

 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
| 2 |
| 3 |
| 2 |
| 3 |
| S1 |
| S2 |
 ,并寫出自變量x的取值范圍.
,并寫出自變量x的取值范圍.查看答案和解析>>
科目:初中數學 來源: 題型:
 平面直角坐標系內有兩條直線l1、l2,直線l1的解析式為y=-
平面直角坐標系內有兩條直線l1、l2,直線l1的解析式為y=-| 2 | 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
|
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 x+1,如果將坐標紙折疊,使直線l1與l2重合,此時點(-2,0)與點(0,2)也重合.
x+1,如果將坐標紙折疊,使直線l1與l2重合,此時點(-2,0)與點(0,2)也重合. )為圓心,CA的長為半徑作圓,過點B任作一條直線(不與y軸重合),與⊙C相交于D、E兩點(點D在點E的下方)
)為圓心,CA的長為半徑作圓,過點B任作一條直線(不與y軸重合),與⊙C相交于D、E兩點(點D在點E的下方)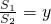 ,求y與x之間的函數關系式
,求y與x之間的函數關系式 ,并寫出自變量x的取值范圍.
,并寫出自變量x的取值范圍.查看答案和解析>>
科目:初中數學 來源:2005年江蘇省鎮江市中考數學試卷(解析版) 題型:解答題
 x+1,如果將坐標紙折疊,使直線l1與l2重合,此時點(-2,0)與點(0,2)也重合.
x+1,如果將坐標紙折疊,使直線l1與l2重合,此時點(-2,0)與點(0,2)也重合. )為圓心,CA的長為半徑作圓,過點B任作一條直線(不與y軸重合),與⊙C相交于D、E兩點(點D在點E的下方)
)為圓心,CA的長為半徑作圓,過點B任作一條直線(不與y軸重合),與⊙C相交于D、E兩點(點D在點E的下方)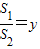 ,求y與x之間的函數關系式,并寫出自變量x的取值范圍.
,求y與x之間的函數關系式,并寫出自變量x的取值范圍.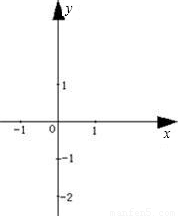
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com