
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的動點(不與A,B重合),過M點作MN∥BC交AC于點N.以MN為直徑作⊙O,并在⊙O內作內接矩形AMPN.令AM=x.

(1)用含x的代數式表示△MNP的面積S;
(2)當x為何值時,⊙O與直線BC相切?
(3)在動點M的運動過程中,記△MNP與梯形BCNM重合的面積為y,試求y關于x的函數表達式,并求x為何值時,y的值最大,最大值是多少?
(1)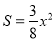 .(0<x<4)(2)x=
.(0<x<4)(2)x=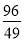 時,⊙O與直線BC相切;(3)y=-
時,⊙O與直線BC相切;(3)y=-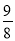 x2+6x-6,當x=
x2+6x-6,當x=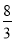 時,y值最大,最大值是2.
時,y值最大,最大值是2.
【解析】
試題分析:(1)由于三角形PMN和AMN的面積相當,那么可通過求三角形AMN的面積來得出三角形PMN的面積,求三角形AMN的面積可根據三角形AMN和ABC相似,根據相似比的平方等于面積比來得出三角形AMN的面積;
(2)當圓O與BC相切時,O到BC的距離就是MN的一半,那么關鍵是求出MN的表達式,可根據三角形AMN和三角形ABC相似,得出MN的表達式,也就求出了O到BC的距離的表達式,如果過M作MQ⊥BC于Q,那么MQ就是O到BC的距離,然后在直角三角形BMQ中,用∠B的正弦函數以及BM的表達式表示出MQ,然后讓這兩表示MQ的含x的表達式相等,即可求出x的值;
(3)要求重合部分的面積首先看P點在三角形ABC內部還是外面,因此可先得出這兩種情況的分界線即當P落到BC上時,x的取值,那么P落點BC上時,MN就是三角形ABC的中位線,此時AM=2,因此可分兩種情況進行討論:
①當0<x≤2時,此時重合部分的面積就是三角形PMN的面積,三角形PMN的面積(1)中已經求出,即可的x,y的函數關系式.②當2<x<4時,如果設PM,PN交BC于E,F,那么重合部分就是四邊形MEFN,可通過三角形PMN的面積-三角形PEF的面積來求重合部分的面積.不難得出PN=AM=x,而四邊形BMNF又是個平行四邊形,可得出FN=BM,也就有了FN的表達式,就可以求出PF的表達式,然后參照(1)的方法可求出三角形PEF的面積,即可求出四邊形MEFN的面積,也就得出了y,x的函數關系式.然后根據兩種情況得出的函數的性質,以及對應的自變量的取值范圍求出y的最大值即可.
試題解析:(1)∵MN∥BC,
∴∠AMN=∠B,∠ANM=∠C.
∴△AMN∽△ABC.
∴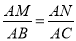 ,
,
即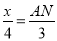 ;
;
∴AN=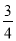 x;
x;
∴S=S△MNP=S△AMN=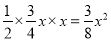 .(0<x<4)
.(0<x<4)
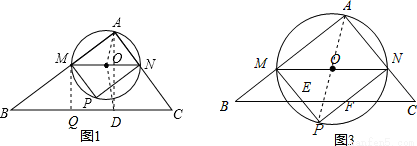
(2)如圖2,設直線BC與⊙O相切于點D,連接AO,OD,則AO=OD=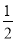 MN.
MN.
在Rt△ABC中,BC=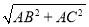 =5;
=5;
由(1)知△AMN∽△ABC,
∴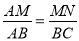 ,
,
即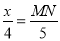 ,
,
∴MN=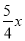
∴OD=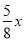 ,
,
過M點作MQ⊥BC于Q,則MQ=OD=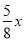 ,
,
在Rt△BMQ與Rt△BCA中,∠B是公共角,
∴△BMQ∽△BCA,
∴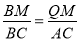 ,
,
∴BM= ,AB=BM+MA=
,AB=BM+MA=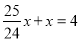
∴x=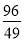 ,
,
∴當x=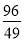 時,⊙O與直線BC相切;
時,⊙O與直線BC相切;
(3)隨點M的運動,當P點落在直線BC上時,連接AP,則O點為AP的中點.
∵MN∥BC,
∴∠AMN=∠B,∠AOM=∠APB,
∴△AMO∽△ABP,
∴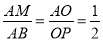 ,
,
∵AM=MB=2,
故以下分兩種情況討論:
①當0<x≤2時,y=S△PMN=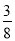 x2,
x2,
∴當x=2時,y最大=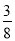 ×4=
×4=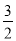 ,
,
②當2<x<4時,設PM,PN分別交BC于E,F,
∵四邊形AMPN是矩形,
∴PN∥AM,PN=AM=x,
又∵MN∥BC,
∴四邊形MBFN是平行四邊形;
∴FN=BM=4-x,
∴PF=x-(4-x)=2x-4,
又∵△PEF∽△ACB,
∴(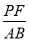 )2=
)2=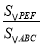 ,
,
∴S△PEF=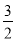 (x-2)2;
(x-2)2;
y=S△MNP-S△PEF=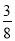 x2-
x2-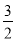 (x-2)2=-
(x-2)2=-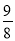 x2+6x-6,
x2+6x-6,
當2<x<4時,y=-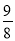 x2+6x-6=-
x2+6x-6=-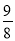 (x-
(x-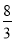 )2+2,
)2+2,
∴當x=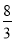 時,滿足2<x<4,y最大=2.
時,滿足2<x<4,y最大=2.
綜上所述,當x=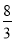 時,y值最大,最大值是2.
時,y值最大,最大值是2.
考點:二次函數綜合題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源:2015屆內蒙古滿洲里市八年級下學期期末考試數學試卷(解析版) 題型:選擇題
如圖,在三角形紙片ABC中,AC=6,∠A=30º,∠C=90º,將∠A沿DE折疊,使點A與點B重合,則折痕DE的長為( )
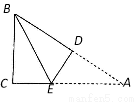
A.1 B.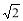 C.
C.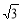 D.2
D.2
查看答案和解析>>
科目:初中數學 來源:2014-2015學年四川省九年級上數學期末模擬數學試卷(解析版) 題型:選擇題
已知點A(-2 ,y1),(-1 ,y2),(3 ,y3)都在反比例函數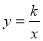 (k>0)的圖象上,則( )
(k>0)的圖象上,則( )
A.y1<y2<y3 B.y3<y2<y1 C.y3 <y1<y2 D.y2<y1<y3
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省泰安市畢業生學業水平模擬二數學試卷(解析版) 題型:填空題
“上升數”是一個數中右邊數字比左邊數字大的自然數(如:34,568,2469等).任取一個兩位數,是 “上升數”的概率是
查看答案和解析>>
科目:初中數學 來源:2014-2015學年山東省泰安市畢業生學業水平模擬二數學試卷(解析版) 題型:選擇題
某電子元件廠準備生產4600個電子元件,甲車間獨立生產了一半后,由于要盡快投入市場,乙車間也加入該電子元件的生產,若乙車間每天生產的電子元件是甲車間的1.3倍,結果用33天完成任務,問甲車間每天生產電子元件多少個?在這個問題中設甲車間每天生產電子元件x個,根據題意可得方程為( )
A.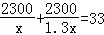
B.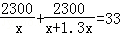
C.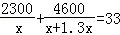
D.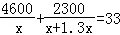
查看答案和解析>>
科目:初中數學 來源:2014-2015學年內蒙古化德縣第三中學九年級上學期期末測試數學試卷(解析版) 題型:解答題
如圖,甲、乙兩人在玩轉盤游戲時,準備了兩個可以自由轉動的轉盤A,B,每個轉盤被分成面積相等的幾個扇形,并在每一個扇形內標上數字.游戲規則:同時轉動兩個轉盤,當轉盤停止后,指針所指區域的數字之和為0時,甲獲勝;數字之和為1時,乙獲勝.如果指針恰好指在分割線上,那么重轉一次,直到指針指向某一區域為止.
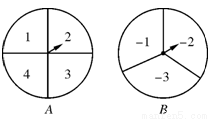
(1)用畫樹狀圖或列表法求乙獲勝的概率;
(2)這個游戲規則對甲、乙雙方公平嗎?請判斷并說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com