
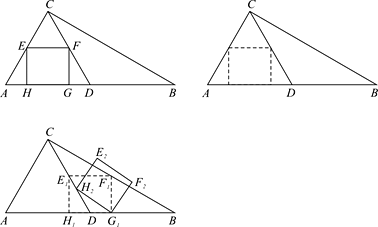
【題目】如圖①,在△ABC中,∠ACB=90°,∠B=30°,AC=1,D為AB的中點,EF為△ACD 的中位線,四邊形EFGH為△ACD的內接矩形(矩形的四個頂點均在△ACD的邊上).
(1)計算矩形EFGH的面積;
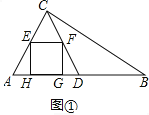
(2)將矩形EFGH沿AB向右平移,F落在BC上時停止移動.在平移過程中,當矩形與△CBD重疊部分的面積為![]() 時,求矩形平移的距離;
時,求矩形平移的距離;
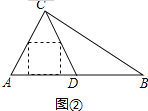
(3)如圖③,將(2)中矩形平移停止時所得的矩形記為矩形![]() ,將矩形
,將矩形![]() 繞
繞![]() 點按順時針方向旋轉,當
點按順時針方向旋轉,當![]() 落在CD上時停止轉動,旋轉后的矩形記為矩形
落在CD上時停止轉動,旋轉后的矩形記為矩形![]() ,設旋轉角為
,設旋轉角為![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)矩形移動的距離為
;(2)矩形移動的距離為![]() 時,矩形與△CBD重疊部分的面積是
時,矩形與△CBD重疊部分的面積是![]() ;(3)
;(3)![]()
【解析】(1)根據已知,由直角三角形的性質可知AB=2,從而求得AD,CD,利用中位線的性質可得EF,DF,利用三角函數可得GF,由矩形的面積公式可得結果;
(2)首先利用分類討論的思想,分析當矩形與△CBD重疊部分為三角形時(0<x≤![]() ),利用三角函數和三角形的面積公式可得結果;當矩形與△CBD重疊部分為直角梯形時(
),利用三角函數和三角形的面積公式可得結果;當矩形與△CBD重疊部分為直角梯形時(![]() <x≤
<x≤![]() ),列出方程解得x;
),列出方程解得x;
(3)作H2Q⊥AB于Q,設DQ=m,則H2Q=![]() m,又DG1=
m,又DG1=![]() ,H2G1=
,H2G1=![]() ,利用勾股定理可得m,在Rt△QH2G1中,利用三角函數解得cosα.
,利用勾股定理可得m,在Rt△QH2G1中,利用三角函數解得cosα.
(1)如圖①,
在![]() 中,
中,
∠ACB=90°,∠B=30°,AC=1,∴AB=2,
又∵D是AB的中點,∴AD=1,![]() .
.
又∵EF是![]() 的中位線,∴
的中位線,∴![]() ,
,
在![]() 中,AD=CD, ∠A=60°,
中,AD=CD, ∠A=60°,
∴∠ADC=60°.
在![]() 中,
中,![]() 60°
60°![]() ,
,
∴矩形EFGH的面積![]() .
.
(2)如圖②,設矩形移動的距離為![]() 則
則![]() ,
,
當矩形與△CBD重疊部分為三角形時,
則![]() ,
,
![]() , ∴
, ∴![]() .(舍去).
.(舍去).
當矩形與△CBD重疊部分為直角梯形時,則![]() ,
,
重疊部分的面積S=![]() , ∴
, ∴![]() .
.
即矩形移動的距離為![]() 時,矩形與△CBD重疊部分的面積是
時,矩形與△CBD重疊部分的面積是![]() .
.
(3)如圖③,作![]() 于
于![]() .
.
設![]() ,則
,則![]() ,又
,又![]() ,
,![]() .
.
在Rt△H2QG1中,![]() ,
,
解之得![]() (負的舍去).
(負的舍去).
∴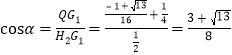 .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】股民王曉宇上周五在股市以收盤價(股市收市時的價格)每股24元購買進某公司股票1000股,周六、周日股市不交易,在接下來的一周交易日內,王曉宇記下該股每日收盤價格相比前一天的漲跌情況如下表:(單位:元)

(1)星期三收盤時,每股是多少元?
(2)已知小明父親買進股票時付了1.5‰的手續費,賣出時需付成交額的1.5‰的手續費和1‰的交易稅,如果他在周五收盤前將全部股票賣出,他的收益情況如何?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,點![]() 為二次函數
為二次函數![]() 圖象的頂點,直線
圖象的頂點,直線![]() 分別交
分別交![]() 軸正半軸,
軸正半軸,![]() 軸于點
軸于點![]() ,
,![]() .
.

(1)判斷頂點![]() 是否在直線
是否在直線![]() 上,并說明理由.
上,并說明理由.
(2)如圖1,若二次函數圖象也經過點![]() ,
,![]() ,且
,且![]() ,根據圖象,寫出
,根據圖象,寫出![]() 的取值范圍.
的取值范圍.
(3)如圖2,點![]() 坐標為
坐標為![]() ,點
,點![]() 在
在![]() 內,若點
內,若點![]() ,
,![]() 都在二次函數圖象上,試比較
都在二次函數圖象上,試比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
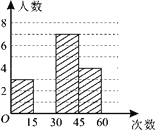
【題目】在大課間活動中,體育老師隨機抽取了七年級甲、乙兩班部分女學生進行仰臥起坐的測試,并對成績進行統計分析,繪制了頻數分布表和統計圖,請你根據圖表中的信息完成下列問題:
(1)頻數分布表中a = ,b= ,并將統計圖補充完整;
(2)如果該校七年級共有女生180人,估計仰臥起坐能夠一分鐘完成30或30次以上的女學生有多少人?
(3)已知第一組中只有一個甲班學生,第四組中只有一個乙班學生,老師隨機從這兩個組中各選一名學生談心得體會,則所選兩人正好都是甲班學生的概率是多少?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知:如圖,在Rt△ABC中,∠C=90°,沿過B點的一條直線BE折疊這個三角形, 使C點與AB邊上的一點D重合.
(1)當∠A滿足什么條件時,點D恰為AB的中點?寫出一個你認為適當的條件,并利用此條件證明D為AB的中點;
(2)在(1)的條件下,若DE=1,求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
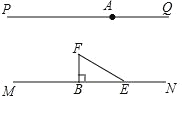
【題目】如圖,直線![]() ,點
,點![]() 在
在![]() 上,直角
上,直角![]() 的直角邊
的直角邊![]() 在
在![]() 上,且
上,且![]()
![]()
![]() .現將
.現將![]() 繞點
繞點![]() 以每秒
以每秒![]() 的速度按逆時針方向旋轉(
的速度按逆時針方向旋轉(![]() 的對應點分別是
的對應點分別是![]() ), 同時,射線
), 同時,射線![]() 繞點
繞點![]() 以每秒
以每秒![]() 的速度按順時針方向旋轉(
的速度按順時針方向旋轉(![]() 的對應點是
的對應點是![]() ).設旋轉時間為
).設旋轉時間為![]() 秒,(
秒,(![]() )在旋轉的過程中,若射線
)在旋轉的過程中,若射線![]() 與邊
與邊![]() 平行時,則
平行時,則![]() 的值為_____.
的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在□ABCD,過點D作DE⊥AB于點E,點F在邊CD上,DF=BE,連接AF,BF.

(1)求證:四邊形BFDE是矩形;
(2)若CF=3,BF=4,DF=5,求證:AF平分∠DAB.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 年
年![]() 月
月![]() 日是全國中小學安全教育日,為了讓學生了解安全知識,增強安全意識,我校舉行了一次“安全知識競賽”.為了了解這次競賽的成績情況,從中抽取了部分學生的成績為樣本,繪制了下列統計圖(說明:A級:90分——100分;B級:75分——89分;C級:60分——74分;D級:60分以下).請結合圖中提供的信息,解答下列問題:
日是全國中小學安全教育日,為了讓學生了解安全知識,增強安全意識,我校舉行了一次“安全知識競賽”.為了了解這次競賽的成績情況,從中抽取了部分學生的成績為樣本,繪制了下列統計圖(說明:A級:90分——100分;B級:75分——89分;C級:60分——74分;D級:60分以下).請結合圖中提供的信息,解答下列問題:
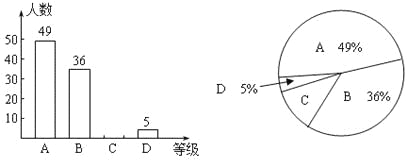
(1)扇形統計圖中C級所在的扇形的圓心角度數是 .
(2)請把條形統計圖補充完整;
(3)若該校共有2000名學生,請你用此樣本估計安全知識競賽中A級和B級的學生共約有多少人?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com