
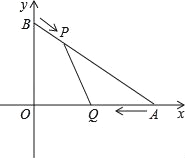
【題目】如圖,在平面直角坐標系xOy中,已知點A(4,0),點B(0,3),點P從點B出發沿BA方向向點A勻速運動,速度為每秒1個單位長度,點Q從點A出發沿AO方向向點O勻速運動,速度為每秒2個單位長度,連接PQ.若設運動的時間為t秒(0<t<2).
(1)求直線AB的解析式;
(2)設△AQP的面積為y,求y與t之間的函數關系式;
(3)是否存在某一時刻t,使線段PQ恰好把△AOB的周長和面積同時平分?若存在,請求出此時t的值;若不存在,請說明理由;
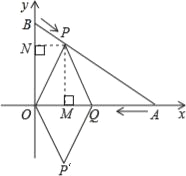
(4)連接PO,并把△PQO沿QO翻折,得到四邊形PQP′O,那么是否存在某一時刻t,使四邊形PQP′O為菱形?若存在,請求出此時點Q的坐標和菱形的邊長;若不存在,請說明理由.
【答案】(1)y=﹣![]() x+3;(2)y=﹣
x+3;(2)y=﹣![]() t2+3t;(3)不存在某一時刻t,使線段PQ恰好把△AOB的周長和面積同時平分,理由見解析;(4)存在某一時刻t,使四邊形PQP'O為菱形,點Q的坐標是(
t2+3t;(3)不存在某一時刻t,使線段PQ恰好把△AOB的周長和面積同時平分,理由見解析;(4)存在某一時刻t,使四邊形PQP'O為菱形,點Q的坐標是(![]() ),菱形PQP′O的邊長為
),菱形PQP′O的邊長為![]() .
.
【解析】
(1)已知了A、B兩點的坐標,可用待定系數法求出直線AB的解析式.
(2)三角形APQ中,底邊AQ的長易知,關鍵是求P點縱坐標的值;過P作PM⊥OA于M,通過構建的相似三角形得出的成比例線段,可求出PM的長.進而可根據三角形的面積公式求出y,t的函數關系式.
(3)可用分析法求解.先假設存在這樣的t值,由于此時PQ將三角形ABO的周長平分,因此BP+BO+OQ=AP+AQ,據此可求出t的值,然后將t的值,代入(2)的函數關系式中,看此時三角形APQ的面積是否等于三角形AOB的面積的一半即可.
(4)如果四邊形OPQP′是菱形,那么需要滿足的條件是OP=PQ,那么PM垂直平分OQ,此時QM=OQ,可借助OA的長來求t的值.過P作PN⊥OB于N,那么三角形BNP和三角形BOA相似,可求得PN的表達式,也就求出了QM,MO的表達式,可根據OA=OM+QM+AQ來求出此時t的值.進而可求出菱形的邊長.
(1)設直線AB的解析式為y=kx+b,
∴![]()
解得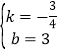 ,
,
∴直線AB的解析式是![]() .
.
(2)在Rt△AOB中,AB=![]() =5,
=5,
依題意,得BP=t,AP=5﹣t,AQ=2t,
過點P作PM⊥AO于M,
∵△APM∽△ABO,
∴![]() ,
,
∴![]() ,
,
∴PM=3﹣![]() t,
t,
∴y=![]() AQPM=
AQPM=![]() 2t(3﹣
2t(3﹣![]() t)=﹣
t)=﹣![]() t2+3t.
t2+3t.
(3)不存在某一時刻
若PQ把△AOB周長平分,則AP+AQ=BP+BO+OQ,
∴(5﹣t)+2t=t+3+(4﹣2t),
解得t=1.
若PQ把△AOB面積平分,則S△APQ=![]() S△AOB,
S△AOB,
∴﹣![]() t2+3t=3,
t2+3t=3,
∵t=1代入上面方程不成立,
∴不存在某一時刻t,使線段PQ把△AOB的周長和面積同時平分.
(4)存在某一時刻t,使四邊形PQP'O為菱形,
過點P作PN⊥BO于N,
若四邊形PQP′O是菱形,則有PQ=PO,
∵PM⊥AO于M,
∴QM=OM,
∵PN⊥BO于N,可得△PBN∽△ABO,
∴![]() ,
,
∴![]() ,
,
∴PN=![]() t,
t,
∴QM=OM=![]() t,
t,
∴![]() t+
t+![]() t+2t=4,
t+2t=4,
∴t=![]() ,
,
∴當t=![]() 時,四邊形PQP′O是菱形,
時,四邊形PQP′O是菱形,
∴OQ=4﹣2t=![]() ,
,
∴點Q的坐標是(![]() ,0).
,0).
∵PM=3﹣![]() t=
t=![]() ,OM=
,OM=![]() t=
t=![]() ,
,
在Rt△PMO中,PO=![]() =
=![]() =
=![]() ,
,
∴菱形PQP′O的邊長為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】一只箱子里共有3個球,其中2個白球,1個紅球,它們除顏色外均相同。
(1)從箱子中任意摸出一個球是白球的概率是多少?
(2)從箱子中任意摸出一個球,不將它放回箱子,攪勻后再摸出一個球,求兩次摸出球的都是白球的概率,并畫出樹狀圖。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】數學課上學習了圓周角的概念和性質:“頂點在圓上,兩邊與圓相交”,“同弧所對的圓周角相等”,小明在課后繼續對圓外角和圓內角進行了探究.
下面是他的探究過程,請補充完整:
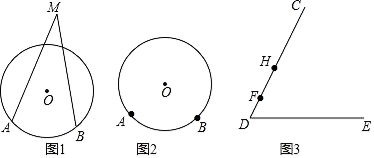
定義概念:頂點在圓外,兩邊與圓相交的角叫做圓外角,頂點在圓內,兩邊與圓相交的角叫做圓內角.如圖1,∠M為![]() 所對的一個圓外角.
所對的一個圓外角.
(1)請在圖2中畫出![]() 所對的一個圓內角;
所對的一個圓內角;
提出猜想
(2)通過多次畫圖、測量,獲得了兩個猜想:一條弧所對的圓外角______這條弧所對的圓周角;一條弧所對的圓內角______這條弧所對的圓周角;(填“大于”、“等于”或“小于”)
推理證明:
(3)利用圖1或圖2,在以上兩個猜想中任選一個進行證明;
問題解決
經過證明后,上述兩個猜想都是正確的,繼續探究發現,還可以解決下面的問題.
(4)如圖3,F,H是∠CDE的邊DC上兩點,在邊DE上找一點P使得∠FPH最大.請簡述如何確定點P的位置.(寫出思路即可,不要求寫出作法和畫圖)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現有兩組相同的撲克牌,每組兩張,兩張牌的牌面數字分別是2和3,從每組牌中各隨機摸出一張牌,稱為一次試驗.
(1)小紅與小明用一次試驗做游戲,如果摸到的牌面數字相同小紅獲勝,否則小明獲勝,請用列表法或畫樹狀圖的方法說明這個游戲是否公平?
(2)小麗認為:“在一次試驗中,兩張牌的牌面數字和可能為4、5、6三種情況,所以出現‘和為4’的概率是![]() ”,她的這種看法是否正確?說明理由.
”,她的這種看法是否正確?說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】春秋旅行社為吸引市民組團去天水灣風景區旅游,推出了如下收費標準:
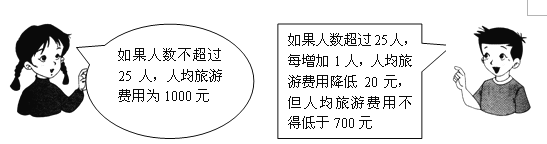 某單位組織員工去天水灣風景區旅游,共支付給春秋旅行社旅游費用27000元,請問該單位這次共有多少員工去天水灣風景區旅游?
某單位組織員工去天水灣風景區旅游,共支付給春秋旅行社旅游費用27000元,請問該單位這次共有多少員工去天水灣風景區旅游?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】類比特殊四邊形的學習,我們可以定義:有一組對角相等而另一組對角不相等的凸四邊形叫做“等對角四邊形”.
探索體驗
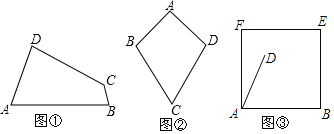
(1)如圖①,已知四邊形ABCD是“等對角四邊形”,∠A≠∠C,∠A=70°,∠B=80°.求∠C,∠D的度數.
(2)如圖②,若AB=AD=a,CB=CD=b,且a≠b,那么四邊形ABCD是“等對角四邊形”嗎?試說明理由.
嘗試應用
(3)如圖③,在邊長為6的正方形木板ABEF上裁出“等對角四邊形”ABCD,若已經確定DA=4,∠DAB=60°,是否在正方形ABEF內(包括邊上)存在一點點C,使四邊形ABCD以∠DAB=∠BCD為等對角的四邊形的面積最大?若存在,試求出四邊形ABCD的最大面積;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=![]() x與雙曲線y=
x與雙曲線y=![]() 交于A、B兩點,且點A的橫坐標為
交于A、B兩點,且點A的橫坐標為![]() .
.
(1)求k的值;
(2)若雙曲線y=![]() 上點C的縱坐標為3,求△AOC的面積;
上點C的縱坐標為3,求△AOC的面積;
(3)在坐標軸上有一點M,在直線AB上有一點P,在雙曲線y=![]() 上有一點N,若以O、M、P、N為頂點的四邊形是有一組對角為60°的菱形,請寫出所有滿足條件的點P的坐標.
上有一點N,若以O、M、P、N為頂點的四邊形是有一組對角為60°的菱形,請寫出所有滿足條件的點P的坐標.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com