
【題目】如圖,平面直角坐標系中,矩形 OABC 的 頂 點 A(0,3),C(- 1,0). 將 矩 形 OABC 繞原點順時針旋轉 900,得到矩形 OA’B’C’.解答下列問題:
(1)求出直線 BB’的函數解析式;
(2)直線 BB’與 x 軸交于點 M、與 y 軸交于點N,拋物線 y = ax2+ bx + c 的圖象經過點C、M、N,求拋物線的函數解析式.
(3)將△MON 沿直線 MN 翻折,點 O 落在點P 處,請你判斷點 P 是否在拋物線上,說明理由.

【答案】(1)y=-![]() ;(2)y=
;(2)y=![]() ;(3)不在.
;(3)不在.
【解析】試題分析:本題考查二次函數的綜合應用,其中涉及到的知識點有待定系數法求函數解析式和函數圖象上點的意義,矩形的性質與面積,函數和方程之間的關系等.要熟練掌握才能靈活運用.
(1)根據四邊形OABC是矩形可知B(-1,3).根據旋轉的性質,得B′(3,1).
把B(-1,3),B′(3,1)代入y=mx+n中,利用待定系數法可解得y=-![]() .
.
(2)由(1)得,N(0,![]() ),M(5,0).設二次函數解析式為y=a
),M(5,0).設二次函數解析式為y=a![]() +bx+c,把C(-1,0),M(5,0),N(0,
+bx+c,把C(-1,0),M(5,0),N(0,![]() )代入得,利用待定系數法解得二次函數解析式為y=
)代入得,利用待定系數法解得二次函數解析式為y=![]()
![]() +2x+
+2x+![]() .
.
(3)過點O作OD⊥MN于點D,由M、N點的坐標,可求出ON、OM的值,進而求得MN的值,然后可求得OD的值,進而求出OP的值,得到P點的坐標,然后將P點的坐標代入拋物線的解析式,即可判斷點P是否在拋物線上.
試題解析:(1)由題意得,B(![]() ,3),
,3),![]() (3,1),
(3,1),
∴直線![]() 的解析式為
的解析式為![]() ;
;
(2)直線![]() 與
與![]() 軸的交點為M(5,0),
軸的交點為M(5,0),
與![]() 軸的交點N(0,
軸的交點N(0,![]() ),
),
設拋物線的解析式為![]() ,
,
∵拋物線過點N,
∴![]() ,
,
∴![]() ,
,
∴拋物線的解析式為![]() =
=![]() ;
;
(3)過點O作OD⊥MN于點D,
∵M(5,0),N(0,![]() ),
),
∴ON=![]() ,OM=5,
,OM=5,
∴MN=![]() ,
,
∴OD=![]() ,
,
∵將△MON沿直線MN翻折,點O落在點P處,
∴OP=![]() ,
,
∴P(2,4)代入拋物線的解析式,
點P不在拋物線上.


科目:初中數學 來源: 題型:
【題目】如圖,已知銳角∠AOB,射線OC不與OA,OB重合,OM,ON分別平分∠AOC,∠BOC.

(1)當OC在∠AOB的內部
①若∠BOC=50°,∠AOC=20°,求∠MON的大小;
②若∠MON=30°,求∠AOB的大小;
(2)當射線OC在∠AOB外部,且∠AOB=80°,請直接寫出∠MON的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】綠水青山就是金山銀山,國家倡導全民植樹。在今年3月12日植樹節當天,某校七年級一班48名學生全部參加了植樹活動,男生每人栽種4株,女生每人栽種3株,全班共栽種170株。
(1)該班男、女生各為多少人?
(2)學校選擇購買甲、乙兩種樹苗,甲樹苗![]() ,乙樹苗
,乙樹苗![]() .如果要使購買樹苗的錢不超過1200元,那么最多可以購買甲樹苗多少株?
.如果要使購買樹苗的錢不超過1200元,那么最多可以購買甲樹苗多少株?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知AO為Rt△ABC的角平分線,∠ACB=90°,![]() ,以O為圓心,OC 為半徑的圓分別交AO,BC于點D,E,連接ED并延長交AC于點F.
,以O為圓心,OC 為半徑的圓分別交AO,BC于點D,E,連接ED并延長交AC于點F.
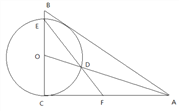
(1)求證:AB是⊙O的切線;
(2)求![]() 的值。
的值。
(3)若⊙O的半徑為4,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知如圖,點 C 在以 AB 為直徑的⊙O 上,點 D 在 AB 的延長線上,∠BCD =∠A.
(1)求證:CD 為⊙O 的切線;
(2)過點 C 作 CE⊥AB 于點 E.若 CE = 2,cos D =![]() ,求 AD 的長.
,求 AD 的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某公司到果品基地購買某種優質水果慰問醫務工作者,果品基地對購買量在3000kg以上(含3000kg)的顧客采用兩種銷售方案.甲方案:每千克9元,由基地送貨上門;乙方案:每千克8元,由顧客自己租車運回.已知該公司租車從基地到公司的運輸費用為5000元.
(1)分別寫出該公司兩種購買方案付款金額y(元)與所購買的水果量x(kg)之間的函數關系式.
(2)當購買量在哪一范圍時,選擇哪種購買方案付款最少?并說明理由
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知x1,x2是一元二次方程(a﹣6)x2+2ax+a=0的兩個實數根.
(1)是否存在實數a,使﹣x1+x1x2=4+x2成立?若存在,求出a的值;若不存在,請你說明理由;
(2)求使(x1+1)(x2+1)為正整數的實數a的整數值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,邊長為2的等邊三角形AEF的頂點E、F分別在BC和CD上,下列結論:①BE=DF;②∠AEB=75°;③CE=2;④S正方形ABCD=2+![]() ,其中正確答案是( )
,其中正確答案是( )

A.①②B.②③C.①②④D.①②③
查看答案和解析>>
科目:初中數學 來源: 題型:
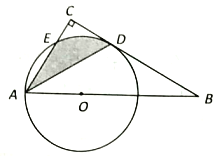
【題目】如圖,點0 為Rt△ABC斜邊AB上的一點,以OA 為半徑的☉O與BC切于點D,與AC 交于點E,連接AD.
(1) 求證: AD平分∠BAC;
(2)若∠BAC= 60°,OA=4,求陰影部分的面積(結果保留π).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com