
【題目】如圖,在矩形紙片![]() 中,已知
中,已知![]() ,
,![]() ,點
,點![]() 在邊
在邊![]() 上移動,連接
上移動,連接![]() ,將多邊形
,將多邊形![]() 沿直線
沿直線![]() 折疊,得到多邊形
折疊,得到多邊形![]() ,點
,點![]() 、
、![]() 的對應點分別為點
的對應點分別為點![]() 、
、![]() .
.
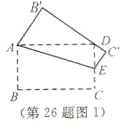
(1)當![]() 恰好經過點
恰好經過點![]() 時(如圖1),求線段
時(如圖1),求線段![]() 的長;
的長;
(2)若![]() 分別交邊
分別交邊![]() 、
、![]() 于點
于點![]() 、
、![]() ,且
,且![]() (如圖2),求
(如圖2),求![]() 的面積;
的面積;
(3)在點![]() 從點
從點![]() 移動到點
移動到點![]() 的過程中,求點
的過程中,求點![]() 運動的路徑長.
運動的路徑長.

【答案】(1) ![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
試題分析:(1)根據折疊的性質可得![]() ,
,![]() ,
,![]() ,
,![]() ,根據勾股定理求得
,根據勾股定理求得![]() ,即可得
,即可得![]() ,易證
,易證![]() ,根據相似三角形的性質即可求得CE的長;(2)如圖2-1,連接AC,根據銳角三角函數求得∠BAC=60°,再求得
,根據相似三角形的性質即可求得CE的長;(2)如圖2-1,連接AC,根據銳角三角函數求得∠BAC=60°,再求得![]() ,根據等腰直角三角形的性質求得
,根據等腰直角三角形的性質求得![]() ,即可求得
,即可求得![]() 的面積;(3)如圖2-2,連接A
的面積;(3)如圖2-2,連接A![]() ,則
,則![]() ,點
,點![]() 的運動路徑是以點A為圓心,以AC為半徑的圓弧,根據弧長公式計算即可.
的運動路徑是以點A為圓心,以AC為半徑的圓弧,根據弧長公式計算即可.
試題解析:
(1)如圖1,由折疊得,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由勾股定理得,![]() ,
,
所以![]() ,
,
因為![]() ,所以
,所以![]() ,
,
又因![]() ,所以
,所以![]()
又![]() ,所以
,所以![]()
所以![]() ,即
,即![]() ,所以
,所以![]()
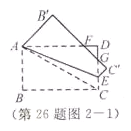
(2)如圖2-1,連接AC,因為∠BAC=![]() ,所以∠BAC=60°,
,所以∠BAC=60°,
故∠DAC=30°,又![]() ,所以
,所以![]() ,
,
由折疊得,![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,![]() ,
,
因為![]() ,所以
,所以![]() ;
;
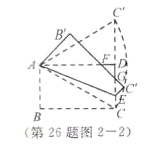
(3) 如圖2-2,連接A![]() ,則
,則![]() ,
,
所以點![]() 的運動路徑是以點A為圓心,以AC為半徑的圓弧;當點E運動到點D時,點
的運動路徑是以點A為圓心,以AC為半徑的圓弧;當點E運動到點D時,點![]() 恰好在CD的延長線上,此時
恰好在CD的延長線上,此時![]() ,
,
所以點的運動路徑長是![]() .
.


 同步練習河南大學出版社系列答案
同步練習河南大學出版社系列答案 同步練習西南師范大學出版社系列答案
同步練習西南師范大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案科目:初中數學 來源: 題型:
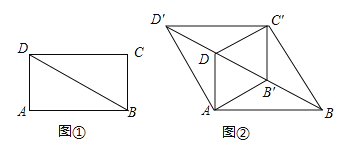
【題目】如圖①,BD是矩形ABCD的對角線,∠ABD=30°,AD=1.將△BCD沿射線BD方向平移到△B'C'D'的位置,使B'為BD中點,連接AB',C'D,AD',BC',如圖②.
(1)求證:四邊形AB'C'D是菱形;
(2)四邊形ABC'D′的周長為 ;
(3)將四邊形ABC'D'沿它的兩條對角線剪開,用得到的四個三角形拼成與其面積相等的矩形,直接寫出所有可能拼成的矩形周長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC,AB的垂直平分線交AB于M,交AC于N.
(1)若∠ABC=70°,則∠MNA的度數是 .
(2)連接NB,若AB=8cm,△NBC的周長是14cm.
①求BC的長;
②在直線MN上是否存在P,使由P、B、C構成的△PBC的周長值最小?若存在,標出點P的位置并求△PBC的周長最小值;若不存在,說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小強與小剛都住在安康小區,在同一所學校讀書.某天早上,小強![]() 從安康小區站乘坐校車去學校,途中需停靠兩個站點才能到達學校站點,且每個站點停留
從安康小區站乘坐校車去學校,途中需停靠兩個站點才能到達學校站點,且每個站點停留![]() 分鐘,校車行駛途中始終保持勻速.當天早上,小剛
分鐘,校車行駛途中始終保持勻速.當天早上,小剛![]() 從安康小區站乘坐出租車沿相同路線出發,出租車勻速行駛,比小強乘坐的校車早
從安康小區站乘坐出租車沿相同路線出發,出租車勻速行駛,比小強乘坐的校車早![]() 分鐘到學校站點.他們乘坐的車輛從安康小區站出發所行駛路程
分鐘到學校站點.他們乘坐的車輛從安康小區站出發所行駛路程![]() (千米)與行駛時間
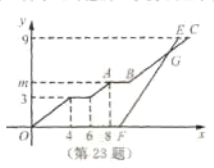
(千米)與行駛時間![]() (分鐘)之間的函數圖象如圖所示.
(分鐘)之間的函數圖象如圖所示.
(1)求點![]() 的縱坐標
的縱坐標![]() 的值;
的值;
(2)小剛乘坐出租車出發后經過多少分鐘追到小強所乘坐的校車?并求此時他們距學校站點的路程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,飛機在一定高度上沿水平直線飛行,先在點![]() 處測得正前方小島
處測得正前方小島![]() 的俯角為
的俯角為![]() ,面向小島方向繼續飛行
,面向小島方向繼續飛行![]()
![]() 到達
到達![]() 處,發現小島在其正后方,此時測得小島的俯角為
處,發現小島在其正后方,此時測得小島的俯角為![]() .如果小島高度忽略不計,求飛機飛行的高度(結果保留根號).
.如果小島高度忽略不計,求飛機飛行的高度(結果保留根號).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com