
【題目】如圖,已知直線y=x+4與兩坐標軸分別交于A、B兩點,⊙C的圓心坐標為 (2,O),半徑為2,若D是⊙C上的一個動點,線段DA與y軸交于點E,則△ABE面積的最小值和最大值分別是 .

【答案】8﹣2![]() 和8+2
和8+2![]()
【解析】首先由一次函數解析式求出OA、OB的長,而△ABE中,BE邊上的高是OA,且OA為定值,所以求△ABE面積的最小值和最大值,轉化為求BE的最小值和最大值。過點A作⊙C的兩條切線AD、AD′,當動點運動到D點時,BE最小,即△ABE面積最小;當動點運動到D′點時,BE最大,即△ABE面積最大。最后根據比例求出BE 、BE′的值,進而求出△ABE面積的最小值和最大值.
解:由y=x+4得:
當x=0時,y=4,當y=0時,x=﹣4,
∴OA=4,OB=4,
∵△ABE的邊BE上的高是OA,
∴△ABE的邊BE上的高是4,
∴要使△ABE的面積最大或最小,只要BE取最大值或最小值即可,
過A作⊙C的兩條切線,如圖,
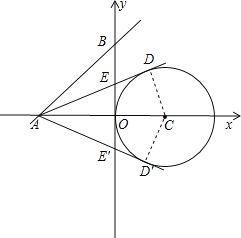
當動點運動到D點時,BE最小,即△ABE面積最小;
當動點運動到D′點時,BE最大,即△ABE面積最大;
∵x軸⊥y軸,OC為半徑,
∴EE′是⊙C切線,
∵AD′是⊙C切線,
∴OE′=E′D′,
設E′O=E′D′=x,
∵AC=4+2=6,CD′=2,AD′是切線,
∴∠AD′C=90°,由勾股定理得:AD′=4![]() ,
,
∴sin∠CAD′=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
解得:x=![]() ,
,
∴BE′=4+![]() ,BE=4﹣
,BE=4﹣![]() ,
,
∴△ABE的最小值是![]() ×(4﹣
×(4﹣![]() )×4=8﹣2
)×4=8﹣2![]() ,
,
最大值是:![]() ×(4+
×(4+![]() )×4=8+2
)×4=8+2![]() ,
,
故答案為:8﹣2![]() 和8+2
和8+2![]() .
.


科目:初中數學 來源: 題型:
【題目】對某班40同學的一次數學成績進行統計,適當分組后80~90分這個分數段的劃記人數為“![]() ”,那么此班在這個分數段的人數占全班人數的百分比是( )
”,那么此班在這個分數段的人數占全班人數的百分比是( )
A.20%
B.40%
C.8%
D.25%
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某土建工程共動用15臺挖運機械,每臺機械每小時能挖土3 m3或運土2 m3.為了使挖土的工作和運土的工作同時結束,若設安排了x臺機械挖土,則x應滿足的方程是( )
A. 2x=3(15-x) B. 3x=2(15-x)
C. 15-2x=3x D. 3x-2x=15
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在邊長為1的小正方形組成的正方形網格中建立如圖片所示的平面直角坐標系,已知格點三角形ABC(三角形的三個頂點都在小正方形上) 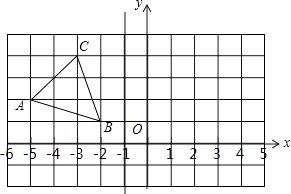
(1)畫出△ABC關于直線l:x=﹣1的對稱三角形△A1B1C1;并寫出A1、B1、C1的坐標.
(2)在直線x=﹣l上找一點D,使BD+CD最小,滿足條件的D點為 .
提示:直線x=﹣l是過點(﹣1,0)且垂直于x軸的直線.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com