
【題目】如圖,矩形ABCD中,AB=5cm,BC=10cm,動(dòng)點(diǎn)M從點(diǎn)D出發(fā),按折線DCBAD方向以3cm/s的速度運(yùn)動(dòng),動(dòng)點(diǎn)N從點(diǎn)D出發(fā),按折線DABCD方向以2cm/s的速度運(yùn)動(dòng).點(diǎn)E在線段BC上,且BE=1cm,若M、N兩點(diǎn)同時(shí)從點(diǎn)D出發(fā),到第一次相遇時(shí)停止運(yùn)動(dòng).
(1)求經(jīng)過幾秒鐘M、N兩點(diǎn)停止運(yùn)動(dòng)?
(2)求點(diǎn)A、E、M、N構(gòu)成平行四邊形時(shí),M、N兩點(diǎn)運(yùn)動(dòng)的時(shí)間;
(3)設(shè)運(yùn)動(dòng)時(shí)間為t(s),用含字母t的代數(shù)式表示△EMN的面積S(cm2).

【答案】(1)經(jīng)過6 s兩點(diǎn)相遇.(2)當(dāng)點(diǎn)A、E、M、N構(gòu)成平行四邊形時(shí),M、N兩點(diǎn)運(yùn)動(dòng)的時(shí)間為4或4.8s.(3)當(dāng)0<t<![]() 時(shí),S =-3t2+
時(shí),S =-3t2+![]() t;當(dāng)
t;當(dāng)![]() ≤t<
≤t<![]() 時(shí),S=S△EMN=
時(shí),S=S△EMN=![]() EMCD=
EMCD=![]() ×(3t-5-1)×5=35-
×(3t-5-1)×5=35-![]() t;當(dāng)
t;當(dāng)![]() <t≤5時(shí),S= t-35;當(dāng)5<t<6時(shí),S =15-
<t≤5時(shí),S= t-35;當(dāng)5<t<6時(shí),S =15-![]() t.
t.
【解析】
(1)由題意可得:M、N兩點(diǎn)同時(shí)從點(diǎn)D出發(fā),到第一次相遇時(shí)共運(yùn)動(dòng)了:2(5+10)=30(cm),則可得t=30÷(2+3)=6;
(2)由題意知,當(dāng)點(diǎn)N在AD邊上運(yùn)動(dòng),點(diǎn)M在BC邊上運(yùn)動(dòng)時(shí),點(diǎn)A、E、M、N才可能組成平行四邊形,然后設(shè)經(jīng)過t秒,四點(diǎn)可組成平行四邊形,①當(dāng)構(gòu)成AEMN時(shí),10-2t=14-3t,②當(dāng)構(gòu)成AMEN時(shí),10-2t=3t-14,繼而求得答案;
(3)分別從當(dāng) 0<t<![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() <
<![]() 時(shí),當(dāng)
時(shí),當(dāng)![]() t<5時(shí),當(dāng)5<t<6時(shí),去分析求解即可求得答案.
t<5時(shí),當(dāng)5<t<6時(shí),去分析求解即可求得答案.
解:(1)∵矩形ABCD中,AB=5cm,BC=10cm,
∴M、N兩點(diǎn)同時(shí)從點(diǎn)D出發(fā),到第一次相遇時(shí)共運(yùn)動(dòng)了:2(5+10)=30(cm),
∴t=30÷(2+3)=6 (s)
答:經(jīng)過6 s兩點(diǎn)相遇.
故答案為:6s.
(2)由題意知,當(dāng)點(diǎn)N在AD邊上運(yùn)動(dòng),點(diǎn)M在BC邊上運(yùn)動(dòng)時(shí),點(diǎn)A、E、M、N才可能組成平行四邊形,
設(shè)經(jīng)過t秒,四點(diǎn)可組成平行四邊形,
①當(dāng)構(gòu)成AEMN時(shí),10-2t=14-3t,
解得t =4;
②當(dāng)構(gòu)成AMEN時(shí),10-2t=3t-14,
解得t=4.8;
答:當(dāng)點(diǎn)A、E、M、N構(gòu)成平行四邊形時(shí),M、N兩點(diǎn)運(yùn)動(dòng)的時(shí)間為4s或4.8s.
故答案為:4s或4.8s.
(3)如圖(1),當(dāng)0<t<![]() 時(shí),點(diǎn)M在線段CD上,
時(shí),點(diǎn)M在線段CD上,
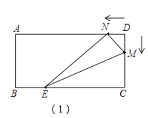
S=S△EMN =S梯形CDNE-S△DMN-S△CEM=![]() ×(2t+9)×5 -
×(2t+9)×5 - ![]() ×2t×3t -
×2t×3t - ![]() ×9×(5-3t)=-3t2+
×9×(5-3t)=-3t2+![]() t;
t;
如圖(2),當(dāng)![]() ≤t<
≤t<![]() 時(shí),點(diǎn)M在線段CE上,
時(shí),點(diǎn)M在線段CE上,
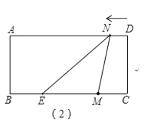
S=S△EMN=![]() EMCD=
EMCD=![]() ×(3t-5-1)×5=35-
×(3t-5-1)×5=35-![]() t;
t;
如圖(3),當(dāng)![]() <t<5時(shí),點(diǎn)M在線段BE上,
<t<5時(shí),點(diǎn)M在線段BE上,
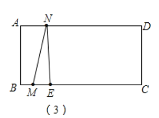
S=S△EMN=![]() MECD =
MECD =![]() ×(3t-14)×5=
×(3t-14)×5=![]() t-35;
t-35;
如圖(4),當(dāng)5<t<6時(shí),點(diǎn)M、N都在線段AB上,
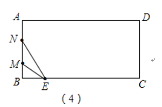
S=S△EMN=![]() MNBE=
MNBE=![]() ×(30-2t-3t)×1=15-
×(30-2t-3t)×1=15-![]() t.
t.
故答案為:當(dāng)0<t<![]() 時(shí),S =-3t2+
時(shí),S =-3t2+![]() t;當(dāng)
t;當(dāng)![]() ≤t<
≤t<![]() 時(shí),S= 35-
時(shí),S= 35-![]() t;當(dāng)
t;當(dāng)![]() <t<5時(shí),S= t-35;當(dāng)5<t<6時(shí),S =15-
<t<5時(shí),S= t-35;當(dāng)5<t<6時(shí),S =15-![]() t.
t.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,坡AB的坡比為1:2.4,坡長AB=130米,坡AB的高為BT.在坡AB的正面有一棟建筑物CH,點(diǎn)H、A、T在同一條地平線MN上.

(1)試問坡AB的高BT為多少米?
(2)若某人在坡AB的坡腳A處和中點(diǎn)D處,觀測(cè)到建筑物頂部C處的仰角分別為60°和30°,試求建筑物的高度CH.(精確到米, ![]() ≈1.73,
≈1.73, ![]() ≈1.41)
≈1.41)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】兩根木條,一根長20cm,另一根長24cm,將它們一端重合且放在同一條直線上,此時(shí)兩根木條的中點(diǎn)之間的距離為( )
A. 2cm B. 4cm C. 2cm或22cm D. 4cm或44cm
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
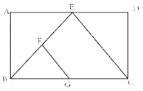
【題目】如圖,在矩形ABCD,BE平分![]() ,交AD于點(diǎn)E,F是BE的中點(diǎn),G是BC的中點(diǎn),連按EC,若
,交AD于點(diǎn)E,F是BE的中點(diǎn),G是BC的中點(diǎn),連按EC,若![]() ,
,![]() ,則FG的長為________。
,則FG的長為________。
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】為了加強(qiáng)學(xué)生的安全意識(shí),某校組織了學(xué)生參加安全知識(shí)競賽,從中抽取了部分學(xué)生成績進(jìn)行統(tǒng)計(jì)(滿分100分,學(xué)生成績?nèi)≌麛?shù)),并按照成績從低到高分成![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五個(gè)小組,繪制統(tǒng)計(jì)圖如下(未完成),解答下列問題:
五個(gè)小組,繪制統(tǒng)計(jì)圖如下(未完成),解答下列問題:

(1)樣本容量為______,頻數(shù)分布直方圖中![]() ______;
______;
(2)扇形統(tǒng)計(jì)圖中![]() 小組所對(duì)應(yīng)的扇形圓心角為______度,并補(bǔ)全頻數(shù)分布直方圖;
小組所對(duì)應(yīng)的扇形圓心角為______度,并補(bǔ)全頻數(shù)分布直方圖;
(3)若成績?cè)?/span>80分以上(不含80分)為優(yōu)秀,全校共有2000名學(xué)生,估計(jì)成績優(yōu)秀的學(xué)生有多少名?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
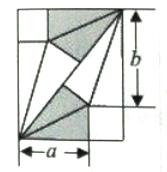
【題目】我國古代數(shù)學(xué)家劉徽將勾股形(古人稱直角三角形為勾股形)分割成一個(gè)正方形和兩對(duì)全等的直角三角形,得到一個(gè)恒等式,后人借助這種分割方法所得的圖形證明了勾股定理,如圖所示的長方形由兩個(gè)這樣的圖形拼成,若![]() ,
,![]() ,則該長方形的面積為__________.
,則該長方形的面積為__________.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,△ABC中,AB=AC=1,∠BAC=45°,△AEF是由△ABC繞點(diǎn)A按順時(shí)針方向旋轉(zhuǎn)得到的.連接BE、CF相交于點(diǎn)D.
(1)求證:BE=CF.
(2)當(dāng)四邊形ACDE為菱形時(shí),求BD的長.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直線y=﹣2x經(jīng)過點(diǎn)P(﹣2,a),點(diǎn)P關(guān)于y軸的對(duì)稱點(diǎn)P′在反比例函數(shù)![]() (k≠0)的圖象上.
(k≠0)的圖象上.
(1)求a的值;
(2)直接寫出點(diǎn)P′的坐標(biāo);
(3)求反比例函數(shù)的解析式.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點(diǎn)A,B分別在x軸、y軸上,點(diǎn)O關(guān)于AB的對(duì)稱點(diǎn)C在第一象限,將△ABC沿x軸正方向平移k個(gè)單位得到△DEF(點(diǎn)B與E是對(duì)應(yīng)點(diǎn)),點(diǎn)F落在雙曲線y=![]() 上,連結(jié)BE交該雙曲線于點(diǎn)G.∠BAO=60°,OA=2GE,則k的值為 ________ .
上,連結(jié)BE交該雙曲線于點(diǎn)G.∠BAO=60°,OA=2GE,則k的值為 ________ .

查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com