
【題目】小明在學習反比例函數的圖像時,他的老師要求同學們根據“探索一次函數![]() 的圖像”的基本步驟,在紙上逐步探索函數
的圖像”的基本步驟,在紙上逐步探索函數![]() 的圖像,并且在黑板上寫出4個點的坐標:
的圖像,并且在黑板上寫出4個點的坐標: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
⑴ 在A、B、C、D四個點中,任取一個點,這個點既在直線![]() 又在雙曲線
又在雙曲線![]() 上的概率是多少?
上的概率是多少?
⑵ 小明從A、B、C、D四個點中任取兩個點進行描點,求兩點都落在雙曲線![]() 上的概率.
上的概率.
【答案】(1)![]() ;⑵
;⑵![]()
【解析】試題分析:(1)把四個點 的坐標分別代入一次函數和反比例函數的解析式可知點B與點D既在直線y=x+1上,又在雙曲線y=![]() 上,據此即可求得任取一個點,這個點既在直線y1=x+1又在雙曲線y2=
上,據此即可求得任取一個點,這個點既在直線y1=x+1又在雙曲線y2=![]() 上的概率.
上的概率.
(2)從A、B、C、D四個點中任意挑選兩個點進行描點,有6種等可能的情況,分別是:AB,AC,AD,BC,BD,CD,其中,“兩點都落在雙曲線![]() 上”有AB、AD、BD 三種情況,從而求得兩點都落在雙曲線
上”有AB、AD、BD 三種情況,從而求得兩點都落在雙曲線![]() 的概率.
的概率.
試題解析:解:(1)把A、B、C、D分別代入y1=x+1和函數y2=![]() 可知:點B與點D既在直線y=x+1上,又在雙曲線y=
可知:點B與點D既在直線y=x+1上,又在雙曲線y=![]() 上,因此任取一個點,既在直線又在雙曲線上的概率是
上,因此任取一個點,既在直線又在雙曲線上的概率是![]() ;
;
(2)由(1)可得,“從A、B、C、D四個點中任意挑選兩個點進行描點”
有6種等可能的情況,分別是:AB,AC,AD,BC,BD,CD,其中,“兩點都落在雙曲線![]() 上”有AB、AD、BD 三種情況.
上”有AB、AD、BD 三種情況.
故兩點都落在雙曲線![]() 的概率是:
的概率是: ![]() .
.


科目:初中數學 來源: 題型:
【題目】我市為加強學生的安全意識,組織了全市學生參加安全知識競賽,為了解此次知識競賽成績的情況,隨機抽取了部分參賽學生的成績,整理并制作出如下的不完整的統計表和統計圖,如圖所示,請根據圖表信息解答以下問題。
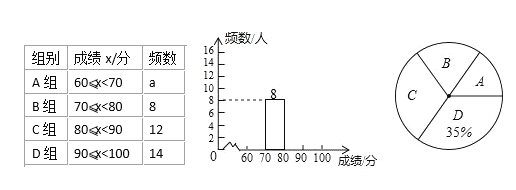
(1)一共抽取了___個參賽學生的成績;表中a=___;
(2)補全頻數分布直方圖;
(3)計算扇形統計圖中“B”對應的圓心角度數;
(4)某校共2000人,安全意識不強的學生(指成績在70分以下)估計有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,圖案由邊長相等的黑、白兩色正方形按一定規律拼接而成,第n個圖案中白色正方形的個數比黑色正方形的個數多_____.(用含有n的代數式表示)
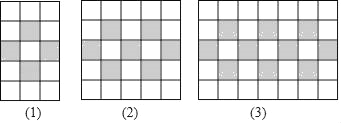
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某市旅游景區有A,B,C,D,E等著名景點,該市旅游部門統計繪制出2018年春節期間旅游情況統計圖(如圖),根據圖中信息解答下列問題:
(1)2018年春節期間,該市A,B,C,D,E這五個景點共接待游客 萬人,扇形統計圖中E景點所對應的圓心角的度數是 ,并補全條形統計圖.
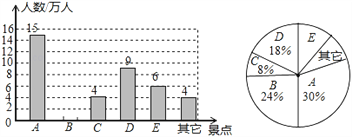
(2)甲,乙兩個旅行團在A,B,D三個景點中隨機選擇一個,這兩個旅行團選中同一景點的概率是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】中國新版高鐵“復興號”率先在北京南站和上海虹橋站雙向首發“復興號”高鐵從某車站出發,在行駛過程中速度![]() (千米/分鐘)與時間
(千米/分鐘)與時間![]() (分鐘)的函數關系如圖所示.
(分鐘)的函數關系如圖所示.

(1)當![]() 時,求
時,求![]() 關于
關于![]() 工的函數表達式,
工的函數表達式,
(2)求點![]() 的坐標.
的坐標.
(3)求高鐵在![]() 時間段行駛的路程.
時間段行駛的路程.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2011年9月1日,長春首屆航空開放日在長春大房身機場正式舉行,空軍八一飛行表演隊的新換裝殲-10飛機,進行了精彩的特技飛行表演,其中一架飛機起飛0.5千米后的高度變化如下表:
高度變化 | 上升4.2 | 下降3.5 | 上升1.4 | 下降1.2 |
記作 | +4.2 | -3.5 | +1.4 | -1.2 |
(1)此時這架飛機飛離地面的高度是多少千米?
(2)如果飛機做特技表演時,有4個規定動作,起飛后高度變化如下:上升3.6干米,下降2.8千米,再上升1.5千米,最后下降0.9千米.若飛機平均上升1干米需消耗6升燃油,平均下降1千米需消耗4升燃油,那么這架飛機在這4個特技表演過程中,一共消耗了多少升燃油?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】新春佳節,電子鞭炮因其安全、無污染開始走俏.某商店經銷一種電子鞭炮,已知這種電子鞭炮的成本價為每盒80元,市場調查發現,該種電子鞭炮每天的銷售量y(盒)與銷售單價x(元)有如下關系:y=﹣2x+320(80≤x≤160).設這種電子鞭炮每天的銷售利潤為w元.
(1)求w與x之間的函數關系式;
(2)該種電子鞭炮銷售單價定為多少元時,每天的銷售利潤最大?最大利潤是多少元?
(3)該商店銷售這種電子鞭炮要想每天獲得2400元的銷售利潤,又想買得快.那么銷售單價應定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,點A的坐標為(0,6),點B在x軸的正半軸上.若點P、Q在線段AB上,且PQ為某個一邊與x軸平行的矩形的對角線,則稱這個矩形為點P、Q的“涵矩形”。下圖為點P、Q的“涵矩形”的示意圖.
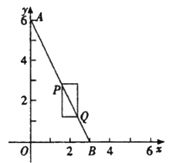
(1)點B的坐標為(3,0);
①若點P的橫坐標為![]() ,點Q與點B重合,則點P、Q的“涵矩形”的周長為 .
,點Q與點B重合,則點P、Q的“涵矩形”的周長為 .
②若點P、Q的“涵矩形”的周長為6,點P的坐標為(1,4),則點E(2,1),F(1,2),G(4,0)中,能夠成為點P、Q的“涵矩形”的頂點的是 .
(2)四邊形PMQN是點P、Q的“涵矩形”,點M在△AOB的內部,且它是正方形;
①當正方形PMQN的周長為8,點P的橫坐標為3時,求點Q的坐標.
②當正方形PMQN的對角線長度為/2時,連結OM.直接寫出線段OM的取值范圍 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,一次函數y1=k1x+2的圖象與反比例函數y2=![]() 的圖象交于點A(4,m)和B(-8,-2),與y軸交于點C.
的圖象交于點A(4,m)和B(-8,-2),與y軸交于點C.

(1)k1=__________,k2=__________;
(2)根據函數圖象可知,當y1>y2時,x的取值范圍是____________;
(3)過點A作AD⊥x軸于點D,點P是反比例函數在第一象限的圖象上一點.設直線OP與線段AD交于點E,當S四邊形ODACS△ODE=31時,求點P的坐標.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com