
【題目】如圖,已知E、F分別是ABCD的邊BC、AD上的點,且BE=DF.

(1)求證:四邊形AECF是平行四邊形;
(2)若∠BAC=90°,AC平分∠EAF,且BC=8cm,求BE的長.
【答案】(1)見解析;(2)4cm.
【解析】
試題分析:(1)利用平行四邊形的性質得出AF∥EC,進而得出AF=EC,進而求出即可;
(2)利用菱形的性質以及三角形內角和定理得出∠2=∠ACE,進而求出∠BAE=∠B,得出BE=AE=CE,再利用直角三角形斜邊上的中線性質得出答案.
(1)證明:∵四邊形ABCD是平行四邊形,
∴AD∥BC,且AD=BC,
∴AF∥EC,
∵BE=DF,
∴AF=EC,
∴四邊形AECF是平行四邊形.
(2)解:∵AC平分∠EAF,
∴∠1=∠2,
∵AD∥BC,
∴∠1=∠ACE,
∴∠2=∠ACE,
∴AE=CE,
∵∠BAC=90°,
∴∠BAE=90°﹣∠1,∠B=90°﹣∠ACE,
∴∠BAE=∠B,
∴AE=BE,
∴BE=AE=CE=![]() BC=4cm.
BC=4cm.


科目:初中數學 來源: 題型:
【題目】如圖,已知直線y=kx-6與拋物線y=ax2+bx+c相交于A,B兩點,且點
A(1,-4)為拋物線的頂點,點B在x軸上.直線AB交y軸于點D,拋物線交y軸于點C.
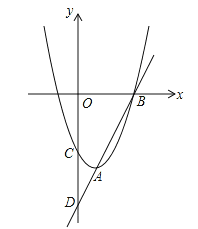
(1)求直線AB的解析式;
(2)求拋物線的解析式;
(3)在y軸上是否存在點Q,使△ABQ為直角三角形?若存在,請求出點Q的坐標;若不存在,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中正確的是( )
A. 數軸上的點與有理數一一對應 B. 數軸上的點與無理數一一對應
C. 數軸上的點與整數一一對應 D. 數軸上的點與實數一一對應
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一次數學課上,老師要求學生根據圖示張鑫與李亮的對話內容,展開如下活動:
活動1:仔細閱讀對話內容

活動2:根據對話內容,提出一些數學問題,并解答.
下面是學生提出的兩個問題,請你列方程解答.
(1)如果張鑫沒有辦卡,她需要付多少錢?
(2)你認為買多少元錢的書辦卡就便宜?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種鉑金飾品在甲、乙兩種商店銷售,甲店標價每克477元,按標價出售,不優惠.乙店標價每克530元,但若買的鉑金飾品重量超過3克,則超出部分可打八折出售.若購買的鉑金飾品重量為x克,其中x>3.
(1)分別列出到甲、乙商店購買該種鉑金飾品所需費用(用含x的代數式表示);
(2)李阿姨要買一條重量10克的此中鉑金飾品,到哪個商店購買最合算.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2016云南省第12題)某校隨機抽查了10名參加2016年云南省初中學業水平考試學生的體育成績,得到的結果如表:
成績(分) | 46 | 47 | 48 | 49 | 50 |
人數(人) | 1 | 2 | 1 | 2 | 4 |
下列說法正確的是( )
A.這10名同學的體育成績的眾數為50
B.這10名同學的體育成績的中位數為48
C.這10名同學的體育成績的方差為50
D.這10名同學的體育成績的平均數為48
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com