
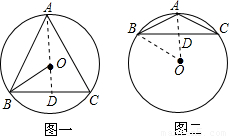
 解:分圓心在內接三角形內和在內接三角形外兩種情況討論,
解:分圓心在內接三角形內和在內接三角形外兩種情況討論,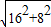 =8
=8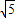 cm;
cm;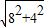 =4
=4 cm.
cm.

 黎明文化寒假作業系列答案
黎明文化寒假作業系列答案 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:初中數學 來源:新課標九年級數學競賽培訓第18講:圓的基本性質(解析版) 題型:解答題
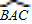 的中點,DE⊥AB于E,求證:BD2-AD2=AB•AC.
的中點,DE⊥AB于E,求證:BD2-AD2=AB•AC.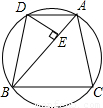
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com