
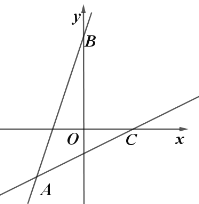
【題目】如圖,在平面直角坐標系中,直線![]() 交
交![]() 軸于點
軸于點![]() ,現將直線
,現將直線![]() 繞點
繞點![]() 順時針方向旋轉45°交
順時針方向旋轉45°交![]() 軸于點
軸于點![]() ,則直線
,則直線![]() 的函數表達式是_________.
的函數表達式是_________.
【答案】![]()
【解析】
過點C作![]() 交AB于點F,根據旋轉
交AB于點F,根據旋轉![]() 可得△FCA是等腰直角三角形,得到FC=AF,設C點的坐標為
可得△FCA是等腰直角三角形,得到FC=AF,設C點的坐標為![]() ,根據A,B的坐標可求出AB所在直線的解析式為
,根據A,B的坐標可求出AB所在直線的解析式為![]() ,根據直線垂直的特點可以求出FC所在的直線解析式為
,根據直線垂直的特點可以求出FC所在的直線解析式為![]() ,聯立可得F的坐標為
,聯立可得F的坐標為![]() ,根據勾股定理可得出FC和AF的值,然后聯立式子可求出C點的坐標,進而求的解析式.
,根據勾股定理可得出FC和AF的值,然后聯立式子可求出C點的坐標,進而求的解析式.
過點C作![]() 交AB于點F.
交AB于點F.
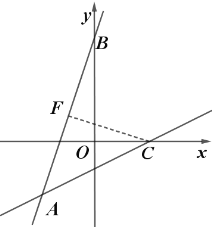
設直線AB所在的直線解析式為![]() ,由題可知
,由題可知![]() ,
,![]() ,得
,得
![]()
設直線CF所在直線的解析式為![]() ,
,![]()
∵直線AB與直線CF垂直
∴![]()
∴![]()
∴![]()
聯立方程組得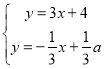
解得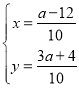
∴F ![]() ,根據題意可得
,根據題意可得
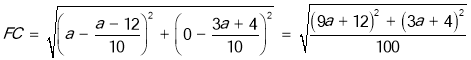
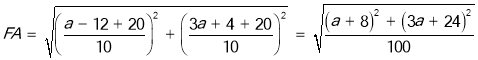
又∵![]()
∴△FCA是等腰直角三角形 ∴FC=FA 得到 整理可得 得到 解方程可得: 所以得到C點的坐標為 設AC所在直線的解析式為 把A,C代入可得 ∴直線AC的函數表達式為 故答案為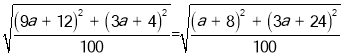
![]()
![]()
![]() (舍去)
(舍去)![]()
![]()
![]()
![]()
![]()


科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.“購買![]() 張彩票就中獎”是不可能事件
張彩票就中獎”是不可能事件
B.“概率為![]() 的事件”是不可能事件
的事件”是不可能事件
C.“任意畫一個六邊形,它的內角和等于![]() ”是必然事件
”是必然事件
D.從![]() 中任取
中任取![]() 個不同的數,分別記為
個不同的數,分別記為![]() 和
和![]() ,那么
,那么![]() 的概率是
的概率是![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,矩形 ABCD 的對角線 AC 與 BD 相交于點 O,CE∥BD, DE∥AC , AD=2![]() , DE=2,則四邊形 OCED 的面積為( )
, DE=2,則四邊形 OCED 的面積為( )

A. 2![]() B. 4 C. 4
B. 4 C. 4![]() D. 8
D. 8
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,拋物線![]() (
(![]() )與
)與![]() 軸交于A、B兩點(點B在A的右側),與
軸交于A、B兩點(點B在A的右側),與![]() 軸交于點C,D是拋物線的頂點.
軸交于點C,D是拋物線的頂點.
(1)當![]() 時,求頂點D 的坐標
時,求頂點D 的坐標
(2)若OD = OB,求![]() 的值;
的值;
(3)設E為A,B兩點間拋物線上的一個動點(含端點A,B),過點E作EH⊥![]() 軸,垂足為H,交直線BC于點F. 記線段EF的長為t,若t的最大值為
軸,垂足為H,交直線BC于點F. 記線段EF的長為t,若t的最大值為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩個種子店都銷售“黃金1號”玉米種子.在甲店,該種子的價格為 5元 / kg,如果一次購買2 kg 以上的種子,超過 2 kg 部分的種子的價格打8折.在乙店,不論一次購買該種子的數量是多少,價格均為4.5 元 / kg.
(1)根據題意,填寫下表:

(2)設一次購買種子的數量為![]() kg(
kg(![]() ). 在甲店購買的付款金額記為
). 在甲店購買的付款金額記為![]() 元,在乙店購買的付款金額為
元,在乙店購買的付款金額為![]() 元,分別求
元,分別求![]() ,
,![]() 關于
關于![]() 的函數解析式;
的函數解析式;
(3) 若在同一店中一次購買種子的付款金額是36元,則最多可購買種子______ kg.若在同一店中一次購買種子10 kg,則最少付款金額是________元.
查看答案和解析>>
科目:初中數學 來源: 題型:
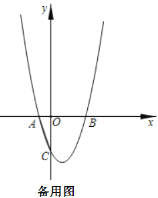
【題目】已知,在平面直角坐標系中,![]() 為坐標原點,拋物線
為坐標原點,拋物線![]()
![]() 分別交
分別交![]() 軸于
軸于![]() 、
、![]() 兩點(點
兩點(點![]() 在點
在點![]() 的側),與
的側),與![]() 軸交于點
軸交于點![]() ,連接
,連接![]() ,
,![]() .
.
(1)如圖1,求![]() 的值;
的值;

(2)如圖2,![]() 是
是![]() 軸上一點(不與點
軸上一點(不與點![]() 、
、![]() 重合),過點
重合),過點![]() 作
作![]() 軸的平行線,交拋物線于點
軸的平行線,交拋物線于點![]() ,交直線
,交直線![]() 于點
于點![]() .
.
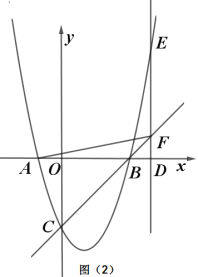
①當點![]() 在點
在點![]() 右側時,連接AF,當
右側時,連接AF,當![]() 時,求
時,求![]() 的長.
的長.
②當點![]() 在運動時,若
在運動時,若![]() 、
、![]() 、
、![]() 中有兩條線段相等,此時點
中有兩條線段相等,此時點![]() 的坐標_________.
的坐標_________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線L:y=x2+bx+c經過點M(2,﹣3),與y軸交于點C(0,﹣3).
(1)求拋物線L的表達式;
(2)試判斷拋物線L與x軸交點的情況;
(3)平移該拋物線,設平移后的拋物線為L′,拋物線L′的頂點記為P,它的對稱軸與x軸交于點Q,已知點N(2,﹣8),怎樣平移才能使得以M、N、P、Q為頂點的四邊形為菱形?
查看答案和解析>>
科目:初中數學 來源: 題型:
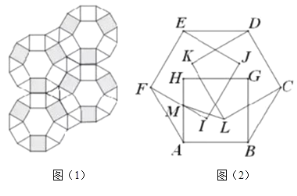
【題目】建筑工人用邊長相等的正六邊形、正方形、正三角形三種瓷磚鋪設地面,正方形瓷磚分黑白兩種顏色,密鋪成圖(1)的形狀.用水泥澆筑前,為方便施工,工人要先把瓷磚按圖1方式先擺放好,一工人擺放時,無意間將3塊黑色正方形瓷磚上翻到一個正六邊形的上面,其中三個正方形的一條邊分別和正六邊形的三條邊重合,如圖(2)所示.按圖(2)方式給各點作上標注,若正方形的邊長![]() ,則
,則![]() _____
_____![]() (不考慮瓷磚的厚度)
(不考慮瓷磚的厚度)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com