
為綠化校園,某校計劃購進A、B兩種樹苗,共21課.已知A種樹苗每棵90元,B種樹苗每棵70元.設購買B種樹苗x棵,購買兩種樹苗所需費用為y元.
(1)y與x的函數關系式為: ;
(2)若購買B種樹苗的數量少于A種樹苗的數量,請給出一種費用最省的方案,并求出該方案所需費用.
【考點】一次函數的應用.
【分析】(1)根據購買兩種樹苗所需費用=A種樹苗費用+B種樹苗費用,即可解答;
(2)根據購買B種樹苗的數量少于A種樹苗的數量,列出不等式,確定x的取值范圍,再根據(1)得出的y與x之間的函數關系式,利用一次函數的增減性結合自變量的取值即可得出更合算的方案.
【解答】解:(1)y=90(21﹣x)+70x=﹣20x+1890,
故答案為:y=﹣20x+1890.
(2)∵購買B種樹苗的數量少于A種樹苗的數量,
∴x<21﹣x,
解得:x<10.5,
又∵x≥1,
∴x的取值范圍為:1≤x≤10,且x為整數,
∵y=﹣20x+1890,k=﹣20<0,
∴y隨x的增大而減小,
∴當x=10時,y有最小值,最小值為:﹣20×10+1890=1690,
∴使費用最省的方案是購買B種樹苗10棵,A種樹苗11棵,所需費用為1690元.
【點評】題考查的是一元一次不等式及一次函數的應用,解決問題的關鍵是讀懂題意,找到關鍵描述語,進而找到所求的量的等量關系和不等關系.


 全優沖刺100分系列答案
全優沖刺100分系列答案 英才點津系列答案
英才點津系列答案科目:初中數學 來源: 題型:
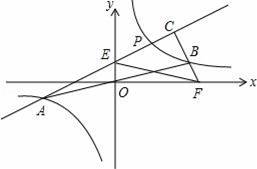
已知雙曲線y=
 (k>0)與直線y=
(k>0)與直線y=
 x(k>0)交于A,B兩點(點A在的B左側)如圖,點P是第一象限內雙曲線上一動點,BC⊥AP于C,交x軸于F,PA交y軸于E,若AE2+BF2=m•EF2,則m= .
x(k>0)交于A,B兩點(點A在的B左側)如圖,點P是第一象限內雙曲線上一動點,BC⊥AP于C,交x軸于F,PA交y軸于E,若AE2+BF2=m•EF2,則m= .

查看答案和解析>>
科目:初中數學 來源: 題型:
九年級一班數學老師對全班學生在模擬考試中A卷成績進行統計后,制成如下的統計表:
| 成績(分) | 80 | 82 | 84 | 86 | 87 | 90 |
| 人數 | 8 | 12 | 9 | 3 | 5 | 8 |
則該班學生A卷成績的眾數和中位數分別是( )
A.82分,82分 B.82分,83分 C.80分,82分 D.82分,84分
查看答案和解析>>
科目:初中數學 來源: 題型:
對于二次函數y=﹣x2+2x.有下列四個結論:①它的對稱軸是直線x=1;②設y1=﹣x12+2x1,y2=﹣x22+2x2,則當x2>x1時,有y2>y1;③它的圖象與x軸的兩個交點是(0,0)和(2,0);④當0<x<2時,y>0.其中正確的結論的個數為( )
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
把拋物線y=x2+1向左平移3個單位,再向下平移2個單位,得到的拋物線表達式為( )
A.y=(x﹣3)2+2 B.y=(x﹣3)2﹣1 C.y=(x+3)2﹣1 D.y=(x﹣3)2﹣2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com