
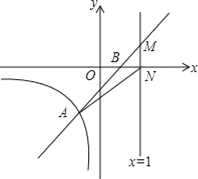
【題目】直線y=kx+b與反比例函數y=![]() (x<0)的圖象交于點A(﹣1,m),與x軸交于點B(1,0)
(x<0)的圖象交于點A(﹣1,m),與x軸交于點B(1,0)
(1)求m的值;
(2)求直線AB的解析式;
(3)若直線x=t(t>1)與直線y=kx+b交于點M,與x軸交于點N,連接AN,S△AMN=![]() ,求t的值.
,求t的值.
【答案】(1)﹣2;(2)y=x﹣1;(3)t=2.
【解析】試題分析:(1)將點A坐標代入y=![]() 可得m的值;
可得m的值;
(2)將點A、B坐標代入y=kx+b可得關于k、b的方程,解方程求出k、b的值,可得直線解析式;
(3)根據直線直線x=t與直線y=kx+b交于點M、與x軸交于點N表示出M、N的坐標,由S△AMN=![]() 可得關于t的方程,解方程可得t的值.
可得關于t的方程,解方程可得t的值.
解:(1)將點A(﹣1,m)代入y=![]() ,得:m=﹣2;
,得:m=﹣2;
(2)由(1)知點A坐標為(﹣1,﹣2),
將點A(﹣1,﹣2)、B(1,0)代入y=kx+b,
得: ![]() ,
,
解得: ![]() ,
,
∴直線AB的解析式為:y=x﹣1;
(3)當x=t時,y=t﹣1,
∴點M坐標為(t,t﹣1),點N坐標為(t,0),
∵S△AMN=![]() ,
,
∴![]() ×(t﹣1)(t+1)=
×(t﹣1)(t+1)=![]() ,
,
解得:t=2或t=﹣2(舍),
∴t=2.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
【題目】要調查某校七年級學生周日的睡眠時間,選取調查對象最合適的是( )
A.選取七年級一個班級的學生
B.選取50名七年級男生
C.選取50名七年級女生
D.隨機選取50名七年級學生
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A(0,1),M(3,2),N(4,4), 動點P從點A出發,沿y
軸以每秒1個單位長的速度向上移動,且過點P的直線l:y=-x+b也隨之移動,設移動時間為t 秒.(直線y = kx+b平移時k不變)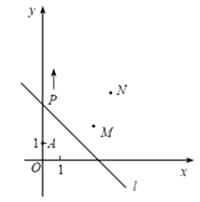
(1)當t=3時,求l 的解析式;
(2)若點M,N位于l 的異側,確定t 的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】學校七年級學生做校服,校服分小號、中號、大號、特大號四種,隨抽取若干名學生調查身高得如下統計分布表:
型號 | 身高x/cm | 人數 | 頻率 |
小號 | 145≤x<155 | 20 | 0.2 |
中號 | 155≤x<165 | a | 0.45 |
大號 | 165≤x<175 | 30 | b |
特大號 | 175≤x<185 | 5 | 0.05 |
(1)這次共抽取__名學生;
(2)a=__,b=__.
查看答案和解析>>
科目:初中數學 來源: 題型:
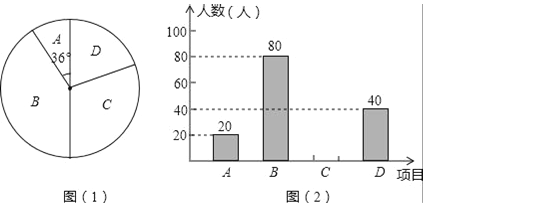
【題目】某學校為了豐富學生課余生活,決定開設以下體育課外活動項目:A.版畫 B.保齡球C.航模 D.園藝種植,為了解學生最喜歡哪一種活動項目,隨機抽取了部分學生進行調查,并將調查結果繪制成了兩幅不完整的統計圖,請回答下列問題:
(1)這次被調查的學生共有 人;
(2)請你將條形統計圖(2)補充完整;
(3)在平時的保齡球項目訓練中,甲、乙、丙、丁四人表現優秀,現決定從這四名同學中任選兩名參加保齡球比賽,求恰好選中甲、乙兩位同學的概率(用樹狀圖或列表法解答)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在Rt△ABC中,∠ACB=90°,AC=BC,D為BC中點,CE⊥AD于E,BF∥AC交CE的延長線于F.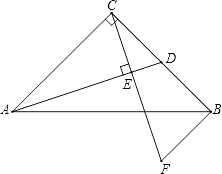
(1)求證:△ACD≌△CBF;
(2)求證:AB垂直平分DF.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com