
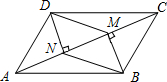
 如圖,AC是平行四邊形ABCD的一條對角線,過點B作BM⊥AC于點M,多點D作DN⊥AC于點N,分別連接BN與DM,求證:BN=DM.
如圖,AC是平行四邊形ABCD的一條對角線,過點B作BM⊥AC于點M,多點D作DN⊥AC于點N,分別連接BN與DM,求證:BN=DM. 分析 由四邊形ABCD是平行四邊形,可得AD=BC,AD∥BC,又由BM⊥AC,DN⊥AC,即可得BM∥DN,∠DNA=∠BMC=90°,然后利用AAS證得△ADN≌△CBM,即可得DN=BM,由有一組對邊相等且平行的四邊形是平行四邊形,證得四邊形BMDN是平行四邊形,即可得出結論.
解答 證明:∵四邊形ABCD是平行四邊形,
∴AD=BC,AD∥BC,
∴∠DAC=∠BCA,
∵BM⊥AC,DN⊥AC,
∴∠AND=∠BMC=90°,BM∥DN,
∵在△ADN和△CBM中,$\left\{\begin{array}{l}{∠AND=∠BMC}&{\;}\\{∠DAN=∠BCM}&{\;}\\{AD=BC}&{\;}\end{array}\right.$,
∴△ADN≌△CBM(AAS),
∴DN=BM,
∴四邊形BMDN是平行四邊形,
∴BN=DM.
點評 本題考查了平行四邊形的性質和全等三角形的性質和判定的應用,主要考查學生運用性質進行推理的能力,題目具有一定的代表性,是一道比較好的題目.


科目:初中數學 來源: 題型:解答題
 根據解答過程填空(寫出推理理由或根據):
根據解答過程填空(寫出推理理由或根據):查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 已知A、B兩地相距40km,甲、乙兩人沿同一公路從A地出發到B地,甲騎摩托車,乙騎自行車,圖中CD、OE分別表示甲、乙離開A地的路程y(km)與時間x(h)的函數關系的圖象,結合圖象解答下列問題.
已知A、B兩地相距40km,甲、乙兩人沿同一公路從A地出發到B地,甲騎摩托車,乙騎自行車,圖中CD、OE分別表示甲、乙離開A地的路程y(km)與時間x(h)的函數關系的圖象,結合圖象解答下列問題.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
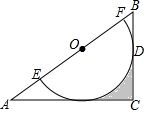 如圖,在Rt△ABC中,∠C=90°,O為AB邊上一點,⊙O交AB于E,F兩點,BC切⊙O于點D,且CD=$\frac{1}{2}$EF=1.
如圖,在Rt△ABC中,∠C=90°,O為AB邊上一點,⊙O交AB于E,F兩點,BC切⊙O于點D,且CD=$\frac{1}{2}$EF=1.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com