
 如圖,?ABCD的對角線AC、BD相交于點O,若S△AOB=3cm2,則S?ABCD=12cm2.
如圖,?ABCD的對角線AC、BD相交于點O,若S△AOB=3cm2,則S?ABCD=12cm2. 分析 先根據等底的兩個三角形面積相等,得:S△AOB=S△AOD,S△BOC=S△DOC,證明△AOB≌△COD(SAS),所以S△AOB=S△COD,可得平行四邊形由對角線分成的四個小三角形的面積相等,可計算平行四邊形的面積.
解答 解:∵四邊形ABCD平行四邊形,
∴OA=OC,OB=OD,
∴S△AOB=S△AOD,S△BOC=S△DOC,
在△AOB和△COD中,
∵$\left\{\begin{array}{l}{AO=OC}\\{∠AOB=∠COD}\\{OB=OD}\end{array}\right.$,
∴△AOB≌△COD(SAS),
∴S△AOB=S△COD,
∵S△AOB=3cm2,
則S?ABCD=4×3=12cm2.
故答案為:12.
點評 本題考查了平行四邊形的性質和面積問題,熟練掌握平行四邊形的性質:平行四邊形的對角線互相平分,明確平行四邊形由對角線分成的四個小三角形的面積相等.


科目:初中數學 來源: 題型:解答題
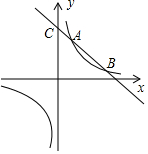 如圖,一次函數y=kx+b的圖象與反比例函數y=$\frac{m}{x}$的圖象交于點A(1,5)和點B,與y軸相交于點C(0,6).
如圖,一次函數y=kx+b的圖象與反比例函數y=$\frac{m}{x}$的圖象交于點A(1,5)和點B,與y軸相交于點C(0,6).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| 加數的個數n | 連續偶數的和S |
| 1 | 2=1×2 |
| 2 | 2+4=6=2×3 |
| 3 | 2+4+6=12=3×4 |
| 4 | 2+4+6+8=20=4×5 |
| 5 | 2+4+6+8+10=30=5×6 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
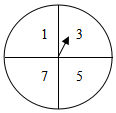 A超市在一次周年慶典當天開展購物抽獎活動,凡當天在該超市購物的顧客,均有一次抽獎機會,抽獎規則如下:將如圖所示的圖形轉盤平均分成四個扇形,分別標上1,3,5,7四個數字,抽獎者連續轉動轉盤兩次,當每次停止后指針所指扇形內的數為每次所得數(若指針指在分界處重轉),當兩次所得數字之和為2時,返現金20元,當兩次所得數字之和為4時,返現金10元,當兩次所得數字之和為6時,返現金5元.
A超市在一次周年慶典當天開展購物抽獎活動,凡當天在該超市購物的顧客,均有一次抽獎機會,抽獎規則如下:將如圖所示的圖形轉盤平均分成四個扇形,分別標上1,3,5,7四個數字,抽獎者連續轉動轉盤兩次,當每次停止后指針所指扇形內的數為每次所得數(若指針指在分界處重轉),當兩次所得數字之和為2時,返現金20元,當兩次所得數字之和為4時,返現金10元,當兩次所得數字之和為6時,返現金5元.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com