
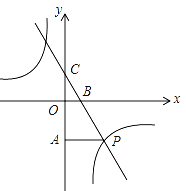
【題目】如圖,一次函數y=kx+3的圖象分別交x軸、y軸于點B、點C,與反比例函數![]() 的圖象在第四象限的相交于點P,并且PA⊥y軸于點A,已知A (0,﹣6),且S△CAP=18.
的圖象在第四象限的相交于點P,并且PA⊥y軸于點A,已知A (0,﹣6),且S△CAP=18.
(1)求上述一次函數與反比例函數的表達式;
(2)設Q是一次函數y=kx+3圖象上的一點,且滿足△OCQ的面積是△BCO面積的2倍,求出點Q的坐標.
【答案】(1)y=![]() ; y=
; y=![]() ;(2)Q1(
;(2)Q1(![]() ), Q2(
), Q2(![]() )
)
【解析】
(1)根據一次函數解析式可得到點C的坐標為(0,3),已知S△CAP=18,可求得點A、點P的坐標,點P在一次函數和反比例函數上,利用待定系數法即可求得函數解析式.
(2)設點Q的坐標(m,![]() m+3),根據一次函數解析式可知點B坐標,結合等底三角形面積性質可得到關于m的一元一次方程,解方程即可求得m值,進而求得Q點坐標.
m+3),根據一次函數解析式可知點B坐標,結合等底三角形面積性質可得到關于m的一元一次方程,解方程即可求得m值,進而求得Q點坐標.
(1)令一次函數y=kx+3中的x=0,則y=3,
即點C的坐標為(0,3),
∴AC=3-(-6)=9.
∵S△CAP=![]() AC·AP=18
AC·AP=18
∴AP=4,
∵點A的坐標為(0,-6),
∴點P的坐標為(4,-6).
∵點P在一次函數y=kx+3的圖象上,
∴-6=4k+3,解得:k=![]()
∵點P在反比例函數![]() 的圖象上,
的圖象上,
∴-6=![]() ,解得:n=-24.
,解得:n=-24.
∴一次函數的表達式為y=![]() x+3,反比例函數的表達式為
x+3,反比例函數的表達式為![]()
(2)令一次函數=y=![]() x+3中的y=0
x+3中的y=0
解得x=![]()
即點B的坐標為(![]() ,0).
,0).
設點Q的坐標為(m,![]() m+3)
m+3)
∵△OCQ的面積是△BCO面積的2倍,
∴|m|=2×![]() ,解得:m=±
,解得:m=±![]() ,
,
∴點Q的坐標為Q1(![]() ), Q2(
), Q2(![]() )
)


 提分百分百檢測卷系列答案
提分百分百檢測卷系列答案 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案科目:初中數學 來源: 題型:
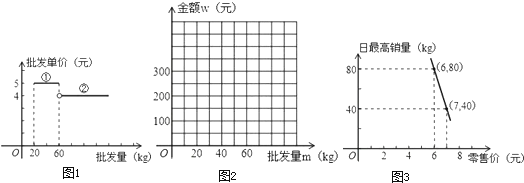
【題目】已知某種水果的批發單價與批發量的函數關系如圖1所示.
(1)請說明圖中①、②兩段函數圖象的實際意義;
(2)寫出批發該種水果的資金金額w(元)與批發量m(kg)之間的函數關系式;在圖2的坐標系中畫出該函數圖象;指出金額在什么范圍內,以同樣的資金可以批發到較多數量的該種水果;
(3)經調查,某經銷商銷售該種水果的日最高銷量與零售價之間的函數關系如圖3所示,該經銷商擬每日售出60kg以上該種水果,且當日零售價不變,請你幫助該經銷商設計進貨和銷售的方案,使得當日獲得的利潤最大.
查看答案和解析>>
科目:初中數學 來源: 題型:
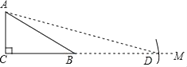
【題目】如何求tan75°的值?按下列方法作圖可解決問題,如圖,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延長CB至點M,在射線BM上截取線段BD,使BD=AB,連接AD,依據此圖可求得tan75°的值為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
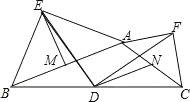
【題目】如圖,在鈍角三角形![]() 中,分別以
中,分別以![]() 和
和![]() 為斜邊向
為斜邊向![]() 的外側作等腰直角三角形
的外側作等腰直角三角形![]() 和等腰直角三角形
和等腰直角三角形![]() ,
,![]() 平分
平分![]() 交
交![]() 于點
于點![]() ,取
,取![]() 的中點
的中點![]() ,
,![]() 的中點
的中點![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,下列結論:①
,下列結論:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正確結論有( )
.其中正確結論有( )
A. ![]() 個B.
個B. ![]() 個C.
個C. ![]() 個D.
個D. ![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,⊙O是△ABC的外接圓,AB=AC=10,BC=12,P是![]() 上的一個動點,過點P作BC的平行線交AB的延長線于點D.
上的一個動點,過點P作BC的平行線交AB的延長線于點D.
(1)當點P在什么位置時,DP是⊙O的切線?請說明理由;
(2)當DP為⊙O的切線時,求線段DP的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著信息技術的迅猛發展,人們去商場購物的支付方式更加多樣、便捷.某校數學興趣小組設計了一份調查問卷,要求每人選且只選一種你最喜歡的支付方式.現將調查結果進行統計并繪制成如下兩幅不完整的統計圖,請結合圖中所給的信息解答下列問題:
(1)這次活動共調查了 人;在扇形統計圖中,表示“支付寶”支付的扇形圓心角的度數為 ;
(2)將條形統計圖補充完整.觀察此圖,支付方式的“眾數”是“ ”;
(3)在一次購物中,小明和小亮都想從“微信”、“支付寶”、“銀行卡”三種支付方式中選一種方式進行支付,請用畫樹狀圖或列表格的方法,求出兩人恰好選擇同一種支付方式的概率.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=10,以AB為直徑的OO與BC相交于點D,與AC相交于點E,DF⊥AC,垂足為F,連接DE,過點A作AG⊥DE,垂足為G,AG與⊙O交于點H.
(1)求證:DF是⊙O的切線;
(2)若∠CAG=25°,求弧AH的長;
(3)若tan∠CDF=![]() ,求AE的長;
,求AE的長;

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校1200名學生發起向貧困山區學生捐款活動,為了解捐款情況,學生會隨機抽取了部分學生的捐款金額,并用得到的數據繪制了如下統計圖①和圖②.
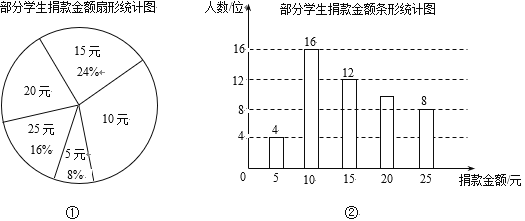
請根據以上信息,解答下列問題:
(1)本次抽樣調查的樣本容量為____;
(2)圖①中“20元”對應扇形的圓心角的度數為_____°;
(3)估計該校本次活動捐款金額為15元以上(含15元)的學生人數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,將拋物線M1:y=ax2+4x向右平移3個單位,再向上平移3個單位,得到拋物線M2,直線y=x與M1的一個交點記為A,與M2的一個交點記為B,點A的橫坐標是﹣3.
(1)求a的值及M2的表達式;
(2)點C是線段AB上的一個動點,過點C作x軸的垂線,垂足為D,在CD的右側作正方形CDEF.
①當點C的橫坐標為2時,直線y=x+n恰好經過正方形CDEF的頂點F,求此時n的值;
②在點C的運動過程中,若直線y=x+n與正方形CDEF始終沒有公共點,求n的取值范圍(直接寫出結果).
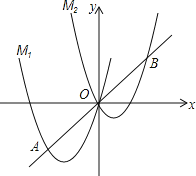
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com